Triangle angle sum
In any triangle, there are always three interior angles. These inside angles always add up to 180°. This rule is very helpful in finding missing angles in a triangle.
Example 1:
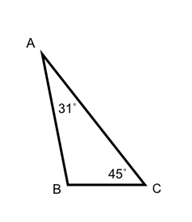 What is \(\angle {\text{B}}\)?
What is \(\angle {\text{B}}\)?
All three angles have to add to 180°, so we have:
\(\angle {\text{B }} + {\text{ 31 }} + {\text{ 45 }} = {\text{ 18}}0\)
\(\angle {\text{B }} + {\text{ 76 }} = {\text{ 18}}0\) (combine like terms)
\(\angle {\text{B }} = {\text{ 1}}0{\text{4}}^\circ \)
Example 2:
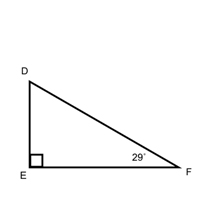
What is \(\angle {\text{D}}\)?
This is a right triangle, so \(\angle {\text{E }} = {\text{ 9}}0^\circ \).
\(\angle {\text{D }} + {\text{ 9}}0{\text{ }} + {\text{ 29 }} = {\text{ 18}}0\)
\(\angle {\text{D }} + {\text{ 119 }} = {\text{ 18}}0\)
\(\angle {\text{D }} = {\text{ 61}}^\circ \)
Example 3: Sometimes, you’ll need to use this property to solve for a variable.
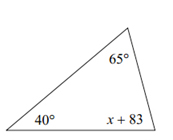 Solve for x.
Solve for x.
We know that all the angles have to equal 180°.
\({\text{65 }} + {\text{ 4}}0{\text{ }} + {\text{ x }} + {\text{ 83 }} = {\text{ 18}}0\)
\({\text{188 }} + {\text{ x }} = {\text{ 18}}0\)
\({\text{x }} = {\text{ }} - {\text{8}}\)
It’s okay that x is a negative number. The angles in a triangle, however, should not be negative. Let’s plug in our answer to make sure this is the case and to check our result.
\({\text{65 }} + {\text{ 4}}0{\text{ }} + {\text{ }}\left( { - {\text{8 }} + {\text{ 83}}} \right){\text{ }} = {\text{ 18}}0\)
\({\text{65 }} + {\text{ 4}}0{\text{ }} + {\text{ 75 }} = {\text{ 18}}0\)
\({\text{18}}0{\text{ }} = {\text{ 18}}0\) ✓
Example 4: Sometimes, we won’t know any of the angles to start with!
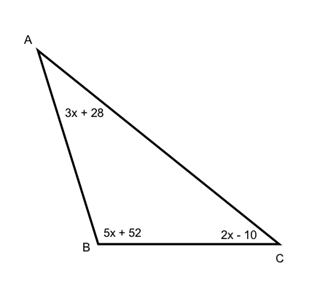
Find all three angles.
We can still use the fact that they have to add to 180°to figure this out.
\({\text{3x }} + {\text{ 28 }} + {\text{ 5x }} + {\text{ 52 }} + {\text{ 2x }}--{\text{ 1}}0{\text{ }} = {\text{ 18}}0\)
\({\text{1}}0{\text{x }} + {\text{ 7}}0{\text{ }} = {\text{ 18}}0\)
\({\text{1}}0{\text{x}} = {\text{11}}0\)
\({\text{x }} = {\text{ 11}}\)
Plug in x = 11 into all the angles to find their measures.
\(\angle {\text{A }} = {\text{ 3x }} + {\text{ 28}}\) ►\({\text{3}}\left( {{\text{11}}} \right){\text{ }} + {\text{ 28}}\) ► \({\text{33 }} + {\text{ 28 }} = {\text{ 61}}^\circ \)
\(\angle {\text{B }} = {\text{ 5x }} + {\text{ 52}}\) ► \({\text{5}}\left( {{\text{11}}} \right){\text{ }} + {\text{ 52}}\) ► \({\text{55 }} + {\text{ 52 }} = {\text{ 1}}0{\text{7}}^\circ \)
\(\angle {\text{C }} = {\text{ 2x }}-{\text{ 1}}0\) ► \({\text{2}}\left( {{\text{11}}} \right){\text{ }}-{\text{ 1}}0\) ► \({\text{22 }}-{\text{ 1}}0{\text{ }} = {\text{ 12}}^\circ \)
Below you can download some free math worksheets and practice.
Find the measure of each angle indicated.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
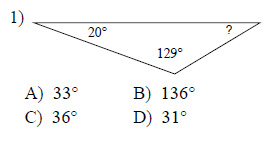
Watch below how to solve this example:
Solve for x.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
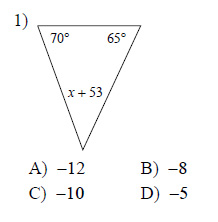
Watch below how to solve this example:
Find the measure of angle A.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
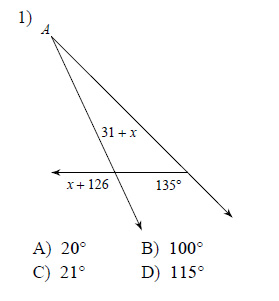
Watch below how to solve this example:


