Centroid
The centroid of the triangle is the point at which the three medians intersect, that is, the centroid is the point of intersection between the three lines, each of which pass through a vertex of the triangle and the midpoint of the opposite leg, as shown in the diagram below:
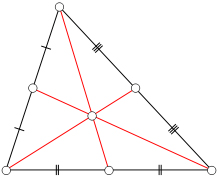
It is relatively easy to find the centroid of a triangle that sits in the coordinate plane. Let a triangle in the plane have vertices with coordinates \(\left( {{x_1},{y_1}} \right)\), \(\left( {{x_2},{y_2}} \right)\), and \(\left( {{x_3},{y_3}} \right)\). Then the centroid of the triangle is given by the coordinates
\(\left( {\Large \frac{{{x_1} + {x_2} + {x_3}}}{3},\Large \frac{{{y_1} + {y_2} + {y_3}}}{3}} \right)\)
EXAMPLE: Find the coordinates of the centroid of the triangle given below
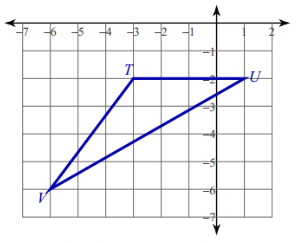
SOLUTION: The three coordinates of the vertices of the triangle are \(\left( { - 6, - 6} \right)\), \(\left( { - 3, - 2} \right)\), and \(\left( {1, - 2} \right)\). Then the centroid has coordinates
\(\left( {\Large \frac{{{x_1} + {x_2} + {x_3}}}{3},\Large \frac{{{y_1} + {y_2} + {y_3}}}{3}} \right) = \left( {\Large \frac{{ - 6 + \left( { - 3} \right) + 1}}{3},\Large \frac{{ - 6 + \left( { - 2} \right) + \left( { - 2} \right)}}{3}} \right)\)
\( = \left( { - \Large \frac{8}{3}, - \Large \frac{{10}}{3}} \right)\)
So the centroid of the triangle is \(\left( { - \Large \frac{8}{3}, - \Large \frac{{10}}{3}} \right)\). Let’s try another example.
EXAMPLE: Find the coordinates of the centroid of the triangle given below
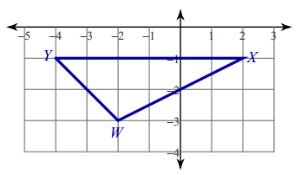
SOLUTION: The coordinates of the vertices of the triangle are \(\left( { - 4, - 1} \right)\), \(\left( { - 2, - 3} \right)\), and \(\left( {2, - 1} \right)\). Then the coordinates of the centroid of the triangle are
\(\left( {\Large \frac{{{x_1} + {x_2} + {x_3}}}{3},\Large \frac{{{y_1} + {y_2} + {y_3}}}{3}} \right) = \left( {\Large \frac{{ - 4 + \left( { - 2} \right) + 2}}{3},\Large \frac{{ - 1 + \left( { - 3} \right) + \left( { - 1} \right)}}{3}} \right)\)
\( = \left( { - \Large \frac{4}{3}, - \Large \frac{5}{3}} \right)\)
So the coordinates of the centroid of the triangle are \(\left( { - \Large \frac{4}{3}, - \Large \frac{5}{3}} \right)\).
So remember that anytime the vertices of the triangle are given as coordinates in the plane, we can easily find the centroid by simply plugging values into our simple formula. It’s that easy!
Below you can download some free math worksheets and practice.
Find coordinates of the centroid of each triangle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
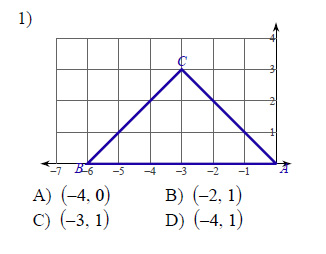
Watch below how to solve this example:
Find coordinates of the centroid of each triangle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
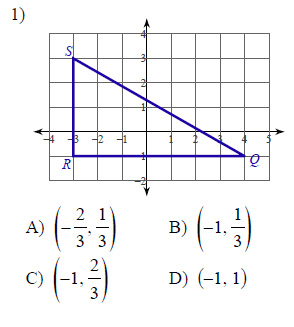
Watch below how to solve this example:
Find the coordinates of the centroid of each triangle given the three vertices.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
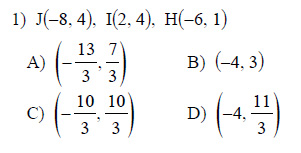
Watch below how to solve this example:


