Classifying triangles
Triangles can be classified in two ways: by their sides and by their angles.
Classifying by sides is a bit easier, so let’s start with that. There are three possibilities for a triangle when dealing with their sides.
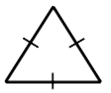
1. Equilateral Triangle ► All three sides are the same length or congruent.
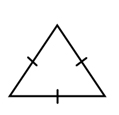
Since each side has one dash through it, it means that they have equal lengths.
2. Isosceles Triangle ► Two sides are congruent.
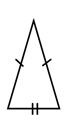
The sides with one dash are the same length, but the side with two dashes is different.
3. Scalene Triangle ► None of the sides are congruent.
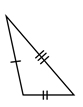
All sides have a different numbers of dashes meaning they all have different lengths.
Now, let’s talk about angles. A triangle has three angles and they always add up to 180°. Let’s review a little bit about angles first.
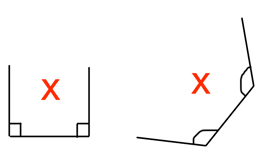
If an angle is less than 90°, it is called an acute angle and looks like:
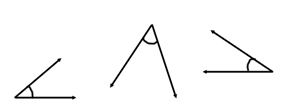
If an angle measures exactly 90°, it is called a right angle and looks like:
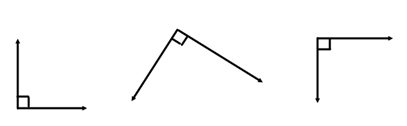
If an angle measures over 90°, it is called an obtuse angle and looks like:
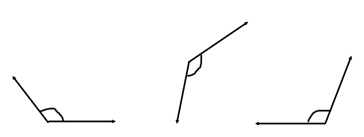
There are also three possibilities of classifying a triangle by their angles.
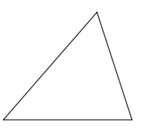
1. Acute Triangle ► ALL three angles are acute.
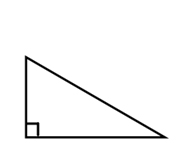
2. Right Triangle ► One angle is a right angle.
3. Obtuse Triangle ► One angle is an obtuse angle.
There’s one more word that you might here regarding angles and it is equiangular, which means that all three angles are congruent. This can only happen in an equilateral triangle.
Triangles are always classified by BOTH their sides and angles. A few examples would be:
 |
 |
 |
 |
| Right Isosceles | Obtuse Isosceles | Obtuse Scalene | Acute Equilateral |
Lastly, here are some statements that are true but can seem a little confusing:
- An equilateral triangle is also an isosceles triangle.
- If the triangle has 3 congruent sides, then is HAS to have 2 congruent sides!
- An equilateral triangle is ALWAYS an acute triangle and equiangular.
- If all sides are congruent, then all angles are congruent. In this case, the angles have to each equal 60°(180/3 equal angles = 60)
- You can never have two right angles or two obtuse angles in one triangle.
- It wouldn’t form a triangle! You would need more sides, and then it’s not a triangle anymore!
Below you can download some free math worksheets and practice.
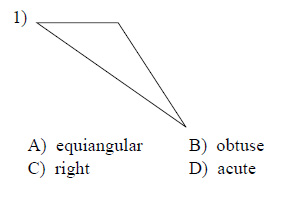
Classify each triangle by its angles.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch bellow how to solve this example:
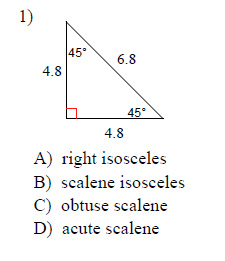
Classify each triangle by its angles and sides.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch below how to solve this example:
Sketch an example of the type of triangle described. Mark the triangle to indicate what information is known. If no triangle can be drawn, write "not possible."
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
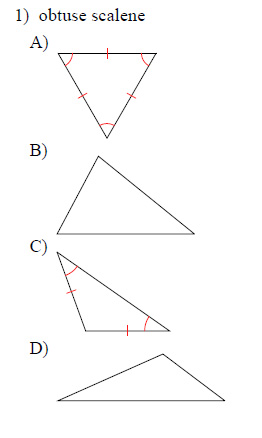
Watch below how to solve this example:


