Tangents
A tangent is a line that just skims the surface of a circle. It hits the circle at one point only.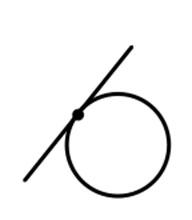
There are two main theorems that deal with tangents. The first one is as follows:
A tangent line of a circle will always be perpendicular to the radius of that circle. It will always form a right angle (90°) with the radius.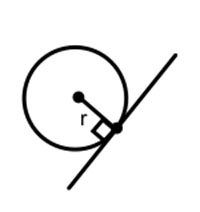
Questions that deal with this theorem usually go hand in hand with the Pythagorean theorem. That’s because you can only use this theorem if you have a right triangle. The Pythagorean theorem is: \({a^2} + {b^2} = {c^2}\) where “c” is always the hypotenuse.
Example 1:
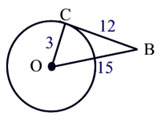 |
Is \({CB}\) a tangent? |
If \({CB}\) is a tangent, then that should be a right triangle which means the Pythagorean theorem will work.
| \(\begin{array}{l} {a^2} + {b^2} = {c^2}\\ {3^2} + {12^2} = {15^2}\\ 9 + 144 = 225\\ 153 \ne 225 \end{array}\) |
It doesn’t work, so \({CB}\) is not a tangent! |
Example 2:
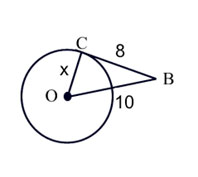 |
\({CB}\) is a tangent. Find x. |
\(\begin{array}{l}
{a^2} + {b^2} = {c^2}\\
{x^2} + {8^2} = {10^2}\\
{x^2} + 64 = 100\\
{x^2} = 36\\
x = 6
\end{array}\)
There is another theorem that deals with tangents as well.
If two tangents to the same circle share a point outside of the circle, then the two tangents are congruent.
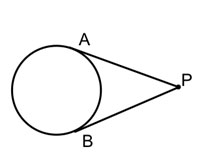 |
If \({AP}\) and \({BP}\) are tangents, then \(\overline {AP} \cong \overline {BP} \) |
Example 1:
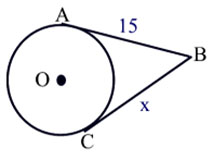 |
\(\overline {AB} \) and \({BC}\) are tangents. Find x. |
Since both lines are tangents and share the point B, then they are equal.
x = 15
Example 2:
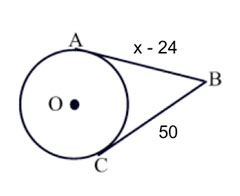 |
\(\overline {AB} \) and \({BC}\) are tangents. Find x. |
These lines are equal as well.
\(\begin{array}{l}
\overline {AB} \cong \overline {BC} \\
x - 24 = 50\\
x = 74
\end{array}\)
Let’s try a tougher one.
Example 3:
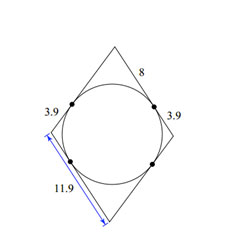 |
All lines are tangents. Find the perimeter of the polygon. |
We have to determine which lines are equal. They have to be tangents that hit the same point.
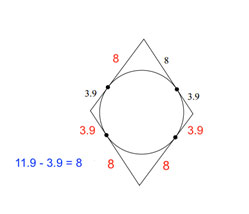 |
To find perimeter, add up all the numbers. 8 + 8 + 3.9 + 3.9 + 8 + 8 + 3.9 + 3.9 = 47.6 |
Let’s try one last example.
Example 4:
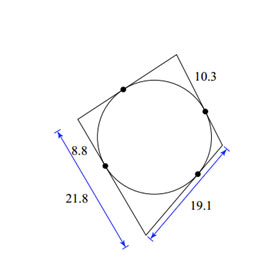 |
All lines are tangents. Find the perimeter of the polygon. |
This one is a little bit tougher. We have to figure it out piece by piece.
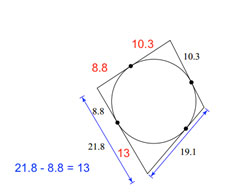 |
Now, we just have a few more pieces to figure out. |
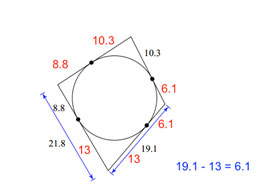 |
Add all the sides. 10.3 + 10.3 + 6.1 + 6.1 + 13 + 13 + 8.8 + 8.8 = 76.4 |
Determine if line AB is tangent to the circle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
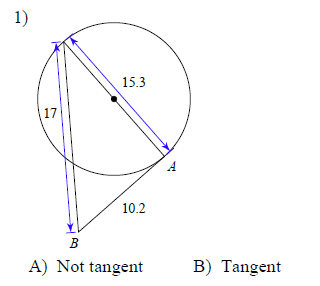
Watch bellow how to solve this example:
Find the perimeter of each polygon. Assume that lines which appear to be tangent are tangent.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
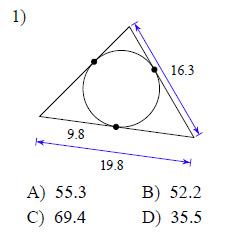
Watch bellow how to solve this example:
Solve for x. Assume that lines which appear to be tangent are tangent.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
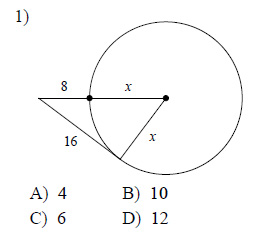
Watch bellow how to solve this example:


