Equations
Radical equations are equations involving a radical expression. They are usually not too difficult to solve as long as you follow three steps:
- Isolate the radical expression (isolate them one at a time if there is more than one)
- Square (or cube, etc.) both sides
- Check for extraneous solutions. Remember that when we multiply both sides of an equation by an expression involving a variable, an extraneous solution may arise (in the case where the variable causes a division by 0 or some other undefined situation… you can do personal research to learn more about why extraneous solutions appear in radical equations).
Let’s jump straight to an example. Solve the equation
\(x = \sqrt {4x} \)
We follow the steps from above. The radical is already isolated, so the first step is complete. Next, since the radical in question is a square root, we will square both sides of the equation to undo it. Then we will solve for \(x\). We have
\(x = \sqrt {4x} \)
\({x^2} = 4x\)
\({x^2} - 4x = 0\)
\(x\left( {x - 4} \right) = 0\)
\(x = 0,4\)
Finally, we must check our solutions to make sure that none of them are extraneous. First we check \(x = 0\). We have
\(\begin{gathered}
0 = \sqrt {4 \cdot 0} \\
0 = \sqrt 0 \\
0 = 0 \\
\end{gathered} \)
The solution checks. Next we check the solution \(x = 4\). We have
\(\begin{gathered}
4 = \sqrt {4 \cdot 4} \\
4 = \sqrt {16} \\
4 = 4 \\
\end{gathered} \)
The solution checks. We have no extraneous solutions. Let’s take a look at another example. We want to solve the equation
\(\sqrt {30 - m} = m\)
Again, we follow the same steps as before. Here the radical is isolated, so the first step is complete. Next, we want to square both sides. We have
\(\sqrt {30 - m} = m\)
\(30 - m = {m^2}\)
\({m^2} + m - 30 = 0\)
\(\left( {m + 6} \right)\left( {m - 5} \right) = 0\)
\(m = - 6,5\)
Finally, we check for extraneous solutions. Check \(m = - 6\). We have
\(\sqrt {30 - \left( { - 6} \right)} = - 6\)
\(\sqrt {36} = - 6\)
\(6 = - 6\)
The solution does not check! So \( - 6\) is an extraneous, or false, solution. We better check the solution \(m = 5\). We have
\(\sqrt {30 - 5} = 5\)
\(\sqrt {25} = 5\)
\(5 = 5\)
The solution checks. So the only solution to the equation \(\sqrt {30 - m} = m\) is \(m = 5\).
Below you can download some free math worksheets and practice.
Solve each equation. Remember to check for extraneous solutions.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
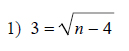
Watch below how to solve this example:
Solve each equation. Remember to check for extraneous solutions.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
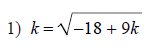
Watch below how to solve this example:
Solve each equation. Remember to check for extraneous solutions.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:


