Graphing systems of inequalities
There are a lot of little elements that you need to know in order to graph a system of inequalities. Much of it is the same as graphing a line, but we will go through all of it one step at a time.
Let’s start out with this system:
\(x + y \geqslant - 1\)
\(y > - 4x + 2\)
Step One: Make sure both inequalities are solved for “y.” This means that “y” must be by itself. The second inequality is ok, but we have to change the first one.
\(x + y \geqslant - 1\)
x –x
\(y \geqslant - 1 - x\)
or \(y \geqslant - x - 1\)
Our system now looks like this:
\(y \geqslant - x - 1\)
\(y > - 4x + 2\)
Step Two: Take one inequality at a time and graph. Let’s take \(y \geqslant - x - 1\) and split this step into two:
Remember:
\(y = mx + b\)
m= slope
b= y-intercept
Your “starting point” is the y-intercept. Find this value on the y-axis and plot a point. So, our starting point is at -1 on the y-axis.
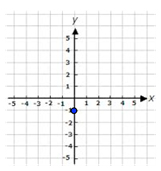
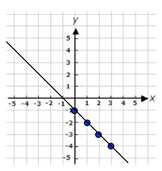
To find more points, we have to use the slope, which is \(\Large \frac{{rise}}{{run}}\). The slope in this example is \(\Large \frac{{ - 1}}{1}\) which means down one, right one. So, let’s go back to our y-intercept and plot some more points.
Step Three: Connect the points with a SOLID LINE if the inequality is \( \leqslant \) (less than or equal to) or \( \geqslant \) (greater than or equal to) and a DOTTED LINE if the inequality is (greater than). This first example is a solid line. So we have:
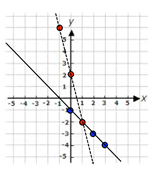
Now, we have to do this all over again with the second inequality!
\(y > - 4x + 2\)
This time our y-intercept is +2 and our slope is \(\frac{{ - 4}}{1}\) which means down 4 and right 1. It is also a DOTTED LINE. So we now have:
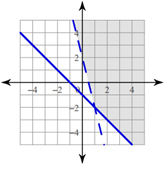
Step Four: We have to shade in part of our graph since there is more than one value that will work in our system of inequalities. For (greater than) or \( \geqslant \) (greater than or equal to), we shade above the line (think of the line as a slide and that’s “above”). In our example, both inequalities are the “above” inequalities so our shading must be above BOTH lines. Our final graph should look like:
Below you can download some free math worksheets and practice.
Sketch the solution to each system of inequalities.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
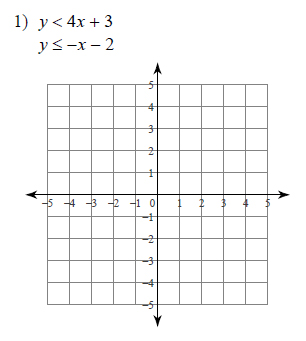
Watch below how to solve this example:
Sketch the solution to each system of inequalities.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
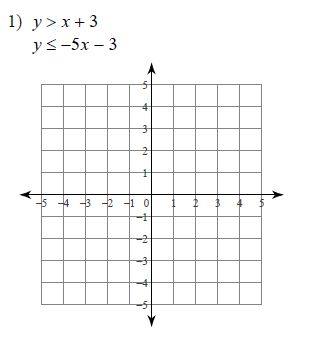
Watch below how to solve this example:
Sketch the solution to each system of inequalities.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
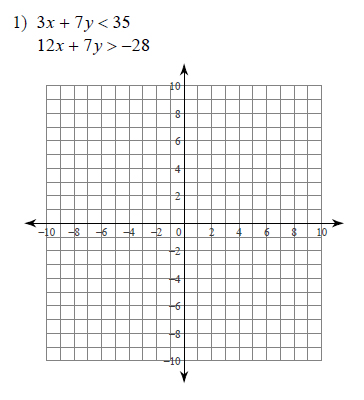
Watch below how to solve this example:


