The Midpoint Formula
Is it possible to find the midpoint between any two points in the plane? That is, given two points \(\left( {{x_1},{y_1}} \right)\) and \(\left( {{x_2},{y_2}} \right)\), is it possible to find the point exactly halfway between those two points? The answer is yes! With the midpoint formula, we can find such a point. The midpoint works similarly to how we find average in mathematics. To find the average between two numbers, you add the numbers, and divide by two. The midpoint formula works similarly. Let’s give the formula, and then jump straight to an example.
Definition: The midpoint of the line segment with endpoints \(\left( {{x_1},{y_1}} \right)\) and \(\left( {{x_2},{y_2}} \right)\) is given by
\(\left( {\Large \frac{{{x_1} + {x_2}}}{2},\Large \frac{{{y_1} + {y_2}}}{2}} \right)\)
Example: Find the midpoint of the line segment with endpoints \(\left( { - 2.8,9.2} \right)\) and \(\left( { - 9.5, - 11.9} \right)\).
Solution: We use the midpoint formula. Here we have \({x_1} = - 2.8\), \({x_2} = - 9.5\), \({y_1} = 9.2\), and \({y_2} = - 11.9\). It’s as simple as plugging in the numbers. Then the midpoint of the line segment with the given endpoints is
\(\left( {\Large \frac{{{x_1} + {x_2}}}{2},\Large \frac{{{y_1} + {y_2}}}{2}} \right) = \left( {\Large \frac{{\left( { - 2.8} \right) + \left( { - 9.5} \right)}}{2},\Large \frac{{\left( {9.2} \right) + \left( { - 11.9} \right)}}{2}} \right)\)
\( = \left( {\Large \frac{{ - 12.3}}{2},\Large \Large \frac{{ - 2.7}}{2}} \right)\)
\( = \left( { - 6.15, - 1.35} \right)\)
Here is a figure illustrating what the midpoint looks like:
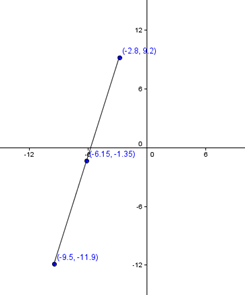 In the figure, you can see the two original endpoints of the segment, as well as the midpoint that we calculated. Visually you should be motivated to believe that \(\left( { - 6.15, - 1.35} \right)\) is indeed the midpoint of that line segment.
In the figure, you can see the two original endpoints of the segment, as well as the midpoint that we calculated. Visually you should be motivated to believe that \(\left( { - 6.15, - 1.35} \right)\) is indeed the midpoint of that line segment.
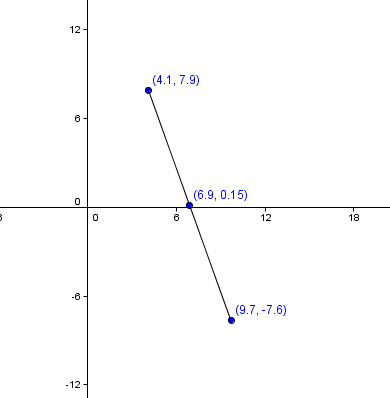
Let’s look at one more example. Find the midpoint of the line segment with endpoints \(\left( {9.7, - 7.6} \right)\) and \(\left( {4.1,7.9} \right)\).
Again we just label our values and plug them in. Here we have \({x_1} = 9.7\), \({x_2} = 4.1\), \({y_1} = - 7.6\) and \({y_2} = 7.9\). Plug these into the midpoint formula:
The midpoint of the line segment with the given endpoints is
\(\left( {\Large \frac{{{x_1} + {x_2}}}{2},\Large \frac{{{y_1} + {y_2}}}{2}} \right) = \left( {\Large \frac{{9.7 + 4.1}}{2},\Large \frac{{ - 7.6 + 7.9}}{2}} \right)\)
\( = \left( {\Large \frac{{13.8}}{2},\Large \frac{{0.3}}{2}} \right)\)
\( = \left( {6.9,0.15} \right)\)
Here is a figure illustrating our result:
Below you can download some free math worksheets and practice.
Find the midpoint of the line segment with the given endpoints.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:
Find the midpoint of the line segment with the given endpoints.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:
Given the midpoint and one endpoint of a line segment, find the other endpoint.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
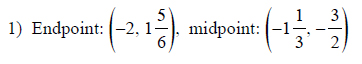
Watch below how to solve this example:


