Exterior Angle Theorem
The Exterior Angle Theorem is not so bad and it’s a very good shortcut to finding the measure of an exterior angle. So, what is an exterior angle?
An exterior angle is when a line is drawn outside of the triangle, extending the angle.
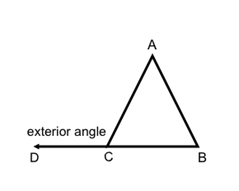
The exterior angle is \(\angle {\text{ACD}}\). All the angles inside the triangle are interior angles.
A little side note: the exterior angle and the adjacent interior angle (the one connected to it) always add up to 180° because together they form a line.
The Exterior Angle Theorem says that an exterior angle of a triangle is equal to the sum of the 2 non-adjacent interior angles.
Taking our above example, \(\angle {\text{ACD}}\) would equal whatever \(\angle {\text{A}}\) + \(\angle {\text{B}}\) equaled because those are the two angles NOT connected to the exterior angle.
Let’s try two fairly basic examples and then try a few tougher ones.
Example 1:
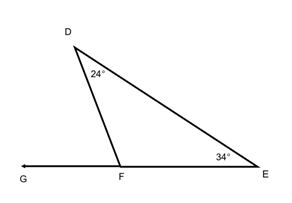
What would \(\angle {\text{DFG}}\) measure?
\(\angle {\text{DFG }} = \angle {\text{D }} + \angle {\text{E}}\)
\(\angle {\text{DFG }} = {\text{ 24 }} + {\text{ 34}}\)
\(\angle {\text{DFG }} = {\text{ 58}}^\circ \)
This next example is a backwards one!
Example 2:
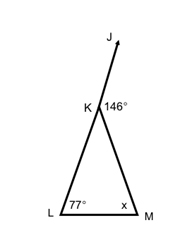
Find the measure of x.
\(\angle {\text{JKM }} = \angle {\text{L }} + \angle {\text{M}}\)
\({\text{146 }} = {\text{ 77 }} + {\text{ x}}\)
\( - {\text{77}} - {\text{77}}\)
____________________
\({\text{69}}^\circ = {\text{ x}}\)
Those will be the two basic types of questions that deal with the Exterior Angle Theorem. They can get tougher when they throw in more than one x! But they are all set up the same way.
Example 3:
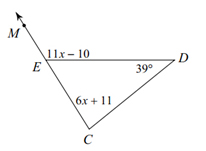
Solve for x.
\(\angle {\text{MED }} = \angle {\text{C }} + \angle {\text{D}}\)
\({\text{11x }}-{\text{ 1}}0{\text{ }} = {\text{ 6x }} + {\text{ 11 }} + {\text{ 39}}\)
\({\text{11x }}-{\text{ 1}}0{\text{ }} = {\text{ 6x }} + {\text{ 5}}0\) (combine like terms)
\({\text{6x}} - {\text{6x}}\) (get variable on one side)
________________________
\({\text{5x }}-{\text{ 1}}0{\text{ }} = {\text{ 5}}0\)
\( + {\text{1}}0 + {\text{1}}0\)
________________________
\({\text{5x}} = {\text{6}}0\)
\({\text{x }} = {\text{ 12}}\)
Example 4:
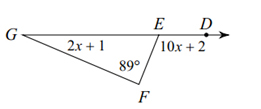
Solve for x.
\(\angle {\text{DEF }} = \angle {\text{G }} + \angle {\text{F}}\)
\({\text{1}}0{\text{x }} + {\text{ 2 }} = {\text{ 2x }} + {\text{ 1 }} + {\text{ 89}}\)
\({\text{1}}0{\text{x }} + {\text{2 }} = {\text{ 2x }} + {\text{ 9}}0\)
\( - {\text{2x}} - {\text{2x}}\)
_____________________________
\({\text{8x }} + {\text{ 2 }} = {\text{ 9}}0\)
\( - {\text{2}} - {\text{2}}\)
\({\text{8x}} = {\text{88}}\)
\({\text{x }} = {\text{ 11}}\)
Below you can download some free math worksheets and practice.
Find the measure of each angle indicated.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
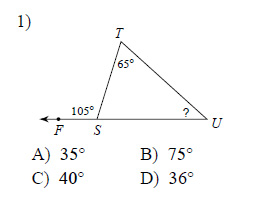
Watch below how to solve this example:
Solve for x.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
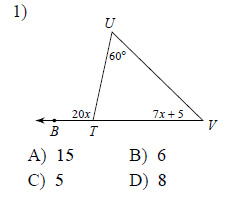
Watch below how to solve this example:
Find the measure of the angle indicated.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
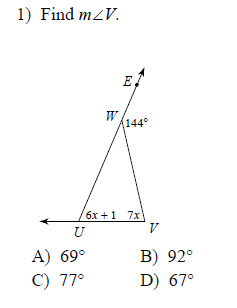
Watch below how to solve this example:


