Dividing integer numbers
In algebra there are two important rules to remember when multiplying and dividing integer numbers:
- If both numbers are positive, the quotient is positive.
- If both numbers are negative, the quotient is positive.
- If the two numbers have different signs, the quotient is negative.
Typically the second bullet point gives algebra students a headache. They ask themselves, “WHY is the product or quotient of two negative numbers positive?!” Well, at the end of this article I have provided a little argument to show you why it’s true. If you don’t follow the argument, that’s okay. You can do some research and find plenty of other explanations of why the product or quotient of two negative numbers is positive.
For now, we will assume that the rule is true. Let’s look at two examples.
Example: Find the quotient \( - 14 \div 7\)
Solution: Here we simply divide \( - 14 \div 7\), which is \(2\). Then we notice in the original problem that one number is negative, and one is positive. So the answer will be negative. The solution is
\(\begin{gathered}
- 14 \div 7 = - \left( {14 \div 7} \right) \\
= - 2 \\
\end{gathered} \)
Example: Find the quotient \( - 110 \div 10\).
Solution: We have
\( - 110 \div 10 = - 11\)
Since one of the numbers is negative and one is positive.
Here is the argument I promised from above. Let a and b be two positive numbers. Then
| \(\left( { - a} \right) + a = 0,\) | additive inverse property |
| \(\left( { - b} \right)*\left[ {\left( { - a} \right) + a} \right] = \left( { - b} \right)*0,\) | multiply both sides by b |
| \(\left( { - b} \right)\left( { - a} \right) + \left( { - b} \right)\left( a \right) = 0,\) | distributive property of multiplication |
| \(\left( { - b} \right)\left( { - a} \right) + \left( { - ba} \right) = 0,\) | since \(\left( { - b} \right)\left( a \right) = \left( { - ba} \right)\) |
| \(\left( { - b} \right)\left( { - a} \right) + \left( { - ba} \right) + \left( {ba} \right) = 0 + \left( {ba} \right),\) | add ba to both sides |
| \(\left( { - b} \right)\left( { - a} \right) + 0 = 0 + \left( {ba} \right),\) | additive inverse property |
| \(\left( { - b} \right)\left( { - a} \right) = ba,\) | identity property |
Chew on that!
Bellow you can download some free math worksheets and practice.
Find each quotient.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch bellow how to solve this example:
Find each quotient.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch bellow how to solve this example:
Find each quotient.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
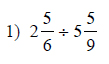
Watch bellow how to solve this example:


