Plotting points
In the coordinate plane we can plot points with the coordinates \(\left( {x,y} \right)\). Let’s look at what an axis system looks like:
So in this coordinate system the \(x\)-axis runs horizontally, increasing from left to right, and the \(y\)-axis runs vertically, increasing from the bottom to the top. Note that both of these axes continue infinitely in both directions, but it is impossible to visually represent an infinite line.
Now let’s try plotting some point \(\left( {x,y} \right)\). Begin by counting the given number of \(x\) units left or right. Then count the given number of \(y\) units up or down. Where those two distances meet is the point with those coordinates \(\left( {x,y} \right)\):
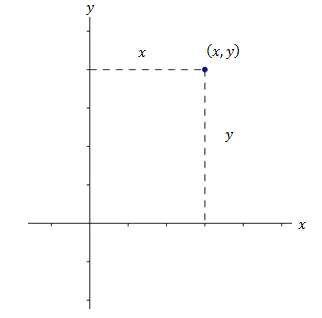
Let’s practice several real examples. In the following example, we are given the coordinates for some points, as well as names for the points: \(Q\), \(R\), \(S\), etc.
Example: Plot each point: \(Q\left( {1,7} \right)\), \(R\left( {10,10} \right)\), \(S\left( {5,9} \right)\), \(T\left( {5,5} \right)\), \(U\left( {8,5} \right)\)
Solution: Here are the plotted points.
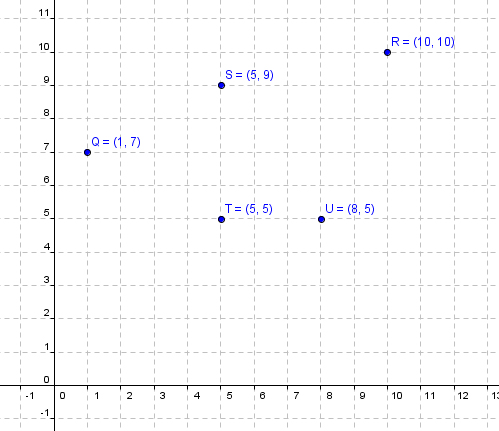
Again, to plot these points, we first count the \(x\) units (the first coordinate of each point) left or right (depending on whether the coordinate is negative or positive. In this example, they’re all positive), and then we count the \(y\) units down or up (again, depending on whether the coordinate is negative or positive). Then we plot the point.
Let’s look at one more example.
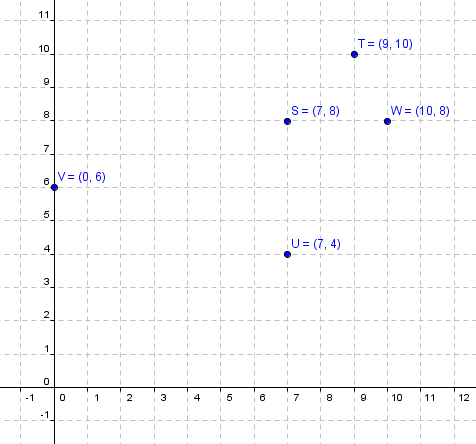
Example: Plot each point: \(S\left( {7,8} \right)\), \(T\left( {9,10} \right)\), \(U\left( {7,4} \right)\), \(V\left( {0,6} \right)\), \(W\left( {10,8} \right)\)
Solution: The points are plotted in the graph.
Below you can download some free math worksheets and practice.
State the quadrant or axis that each point lies in.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:
Plot each point.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
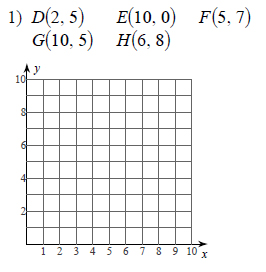
Watch below how to solve this example:
State the coordinates of each point.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
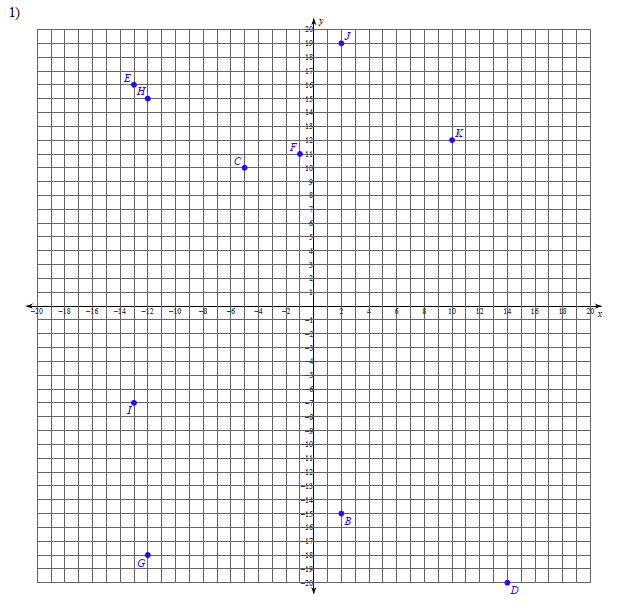
Watch below how to solve this example:


