Adding and subtracting
Adding and subtracting can be a very easy process especially if you think back to when you first learned to add:
Example:
“If you have 2 apples and I give you 3 more, how many apples do you have?”
But is can get difficult sometimes unless you know what you’re doing and how to make it easier.
The addition/subtraction of radical expressions can be done just like “regular” numbers; however, in some cases you may not be able to simplify all the way down to one number.
To add or subtract radicals the must be like radicals. Like radicals have the same root and radicand.

Examples of like radicals are: \((\sqrt{2}, 5\sqrt{2}, -4\sqrt{2}) \) or \( ( \sqrt[3]{15}, 2\sqrt[3]{15}, -9\sqrt[3]{15}) \)
Simplify:
\(3\sqrt{2} + 2\sqrt{2}\)
The terms in this expression contain like radicals so can therefore be added. Now if you look at the radical part in the expression like the apple in the opening example about adding, you can get a better understanding of how to treat the radicals. In other words:
3 “apples” + 2 “apples” = (3+2) “apples” or 5 “apples” (Now switch “apples” to \(\sqrt{2}\)).
\(3\sqrt{2} + 2\sqrt{2} = (3 + 2)\sqrt{2} = 5\sqrt{2}\)
Simplify:
\(\sqrt{3} + 5\sqrt{3}\)
For the purpose of this explanation I will put the understood 1 in front of the first term giving me:
\(1\sqrt{3} + 5\sqrt{3}\)
(like radical terms can be combined)
\((1 + 5)\sqrt{3}\)
\(6\sqrt{3}\)
Simplify:
\(-8\sqrt{5} + 5\sqrt{5}\) (like radical terms)
\((-8 + 5)\sqrt{5}\)
\(-3\sqrt{5}\)
Now what happens if we have unlike radicals?
Simplify: \(\sqrt{16} + \sqrt{4}\) (unlike radicals, so you can’t combine them…..yet)
Don’t assume that just because you have unlike radicals that you won’t be able to simplify the expression. Therefore, in every simplifying radical problem, check to see if the given radical itself, can be simplified.
In this problem, the radicals simplify completely: \(\sqrt{16} + \sqrt{4} = 4 + 2 = 6\)
Simplify:
\(2\sqrt{25} + 5\sqrt{9}\)
Think here that you have 2 square roots of 25 and 5 square roots of 9.
Now,\(\sqrt{25} = 5\) and \(\sqrt{9} = 3\) so,
\(2\sqrt{25} + 5\sqrt{9} = 2\cdot 5 + 5\cdot 3 = 10 + 15 = 25\)
Sometimes simplification isn’t as apparent.
Simplify:
\(-2\sqrt{2} + \sqrt{18}\)
\(\sqrt{18}\) can be simplified (as seen in an earlier lesson): \(\sqrt{9\cdot 2} = \sqrt{9}\cdot \sqrt{2} = 3\sqrt{2}\)
Putting that back into the problem above yields:
\(-2\sqrt{2} + 3\sqrt{2} = -1\sqrt{2} = \sqrt{2}\)
Simplify:
\(3\sqrt{7} - 2\sqrt{28} + 4\sqrt{7}\) (start by ensuring all radicals are simplified)
\(3\sqrt{7} - 2\sqrt{4\cdot 7} + 4\sqrt{7}\)
\(3\sqrt{7} - 2\cdot 2\sqrt{7} + 4\sqrt{7}\)
\(3\sqrt{7} - 4\sqrt{7} + 4\sqrt{7}\)
\((3 - 4 + 4)\sqrt{7} = 3\sqrt{7}\)
So you’re doing a problem and you’ve simplified your radicals; however, they’re not all alike. WHAT DO YOU DO NOW?!?!? Well, nothing………sort of.
Simplify:
\(3\sqrt{3} + 2\sqrt{7} - \sqrt{3}\) (you notice that two of the three are alike, so combine the two like radical terms)
\(3\sqrt{3} - 1\sqrt{3} + 2\sqrt{7}\)
\((3 - 1)\sqrt{3} + 2\sqrt{7}\)
\(2\sqrt{3} + 2\sqrt{7}\) and that’s the answer! It cannot be simplified any further.
Bellow you can download some free math worksheets and practice.
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
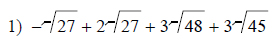
Watch below how to solve this example:


