Mixture word problems
Word problems that deal with mixing different percentages of solutions can be pretty difficult at first. You need to be able to interpret and separate the information that they are giving you. Let’s see what this looks like using an example.
Example 1:
3 ml of a sugar solution was mixed with 1 ml of a 56% sugar solution to make a 65% sugar solution. Find the percent of concentration of the first solution.
Let’s organize the information (change the percents to decimals by dividing by 100):
There are 3 ml of solution with an x percentage -> 3 · x = 3x
There is 1 ml of solution with a .56 percentage -> 1 · .56 = .56
There is 4 ml of solution in total with a .65 percentage -> 4 · .65 = 2.6
To solve for x, we need to add the two solutions to equal the total solution.
3x + .56 = 2.6
- .56 - .56
3x = 2.04
3x = 2.04 / 3
x = .68
The first solution had a percentage of 68%.
Example 2:
Ted mixed together 3 gallons. of Brand A fruit drink and 9 gallons of Brand B fruit drink which contains 44% fruit juice. Find the percent of fruit juice in Brand A if the mixture contained 36% fruit juice.
Let’s organize the information:
There are 3 gallons of Brand A fruit drink with an x percentage -> 3 · x = 3x
There are 9 gallons of Brand B fruit drink with a .44 percentage -> 9 · .44 = 3.96
There is 12 gallons of fruit drink in total with a .36 percentage -> 12 · .36 = 4.32
Add the two brands of fruit drink to equal the total mixture.
3x + 3.96 = 4.32
- 3.96 - 3.96
3x = .36
3x = .36 /3
x = .12
Brand A fruit drink contained 12% fruit juice.
Below you can download some free math worksheets and practice.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
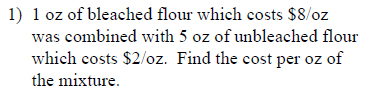
Watch bellow how to solve this example:
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
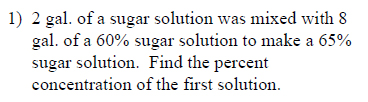
Watch bellow how to solve this example:
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
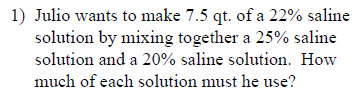
Watch bellow how to solve this example:


