Understanding the discriminant
Let’s review what we know about the standard form of a quadratic equation.
\(y = ax^2 + bx + c\)
We will need the a, b, and c in order to work with something that is called the discriminant.
Every quadratic equation falls into one of three possibilities. The first one is when the equation has two real solutions (also called x-intercepts, roots or zeros.) This means the parabola crosses the x-axis twice, like the following:
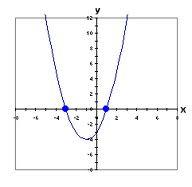
Another possibility is if the quadratic equation only has one real solution. This graph shows the parabola only hitting the x-axis once:
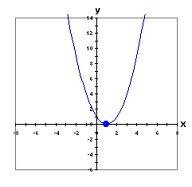
And the last possibility is if the quadratic equation has no real solutions. Can you guess how many times this graph would cross the x-axis? None!
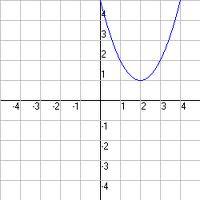
The discriminant comes in handy because it tells us which one of these categories a quadratic equation belongs to. There is a formula that you will need to find this discriminant. It is:
\(b^2 - 4ac\)
This is your same a, b, and c from the standard form above! The following are the rules that will decipher what your discriminant is telling you.
- If the discriminant equals a positive number ► there are two real solutions
- If the discriminant equals zero ► there is one real solution
- If the discriminant equals a negative number ► there are no real solutions
Let’s try one. We are given the quadratic equation:
\(9x^2 - 6x + 1 = 0\)
\(a = 9, b = -6, c = 1\)
\(b^2 - 4ac\)
\((-6)^2 - 4(9)(1)\)
\(36-36\)
\(0\)
The discriminant equals zero, which means that this equation will have one real solution!
One step tougher:
\(11x^2 - 7x - 16 = -13\)
This one is different because it’s not equal to zero. We can’t figure out our a, b, and c until it is equal to zero. So let’s get rid of that -13 by adding 13 to both sides.
\(\array{ 11x^2 - 7x - 16 =& -13 \cr +13 & +13}\)
\(11x^2 - 7x - 3 = 0\)
\(a = 11, b = -7, c = -3\)
\(b^2 - 4ac\)
\((-7)^2 - 4(11)(-3)\)
\(49 - 132\)
\(-83\)
This is a negative number, which means that this equation will have no real solutions!
One more for good measure:
\(-18r^2 - 6r - 2 = -4r^2 - 2\)
It’s not equal to zero, so let’s fix that first:
\(\array{ -18r^2 - 6r - 2 =& -4r^2 - 2 \cr +4r^2 & +4r^2}\)
\(\array{ -14r^2 - 6r - 2 =& - 2 \cr +2 & +2}\)
\(-14r^2 - 6r = 0\)
Oh no! The value of “c” disappeared! It’s ok, it just means that c = 0. So we now have:
\(a = -14, b = -6, c = 0\)
\(b^2 - 4ac\)
\((-6)^2 - 4(-14)(0)\)
\(36-0\)
\(36\)
This is a positive number, which means that this equation will havetwo real solutions!
Bellow you can download some free math worksheets and practice.
Find the value of the discriminant of each quadratic equation.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:
Find the discriminant of each quadratic equation then state the number and type of solutions.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:
Find the discriminant of each quadratic equation then state the number and type of solutions.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:


