Slope and lines
Slopeis the measure of the “steepness” of a line. It can rise or fall at a fast rate or a slow, gradual rate. There are a few general things that you need to know about slope.

This line is increasing. Always go from the left to right and think if this were a hill, would you have to walk up it or down it? Up! So, any line that you would have to walk up is increasing and a positive slope.

This would be a hill that you would walk down, right? This line is decreasing and is a negative slope.

Well, you wouldn’t be walking up or down on a hill like this. A horizontal line always has a zero slope because it has no steepness!

You wouldn’t even be able to get onto this hill! It would be impossible! The “math” way of saying something is impossible is undefined. All vertical lines have an undefined slope.
These facts are very helpful, but we want to be able to find the value of the slope also.
\(slope = \frac{{rise}}{{run}}\) rise is your “up or down” & run is your “left or right”
If they give you a graph, we can simply count from one point to another.
Example 1:
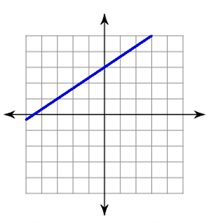
This is a positive slope.
Your rise is 2 and your run is 3.
\(slope = \Large \frac{{rise}}{{run}} = \Large \frac{2}{3}\)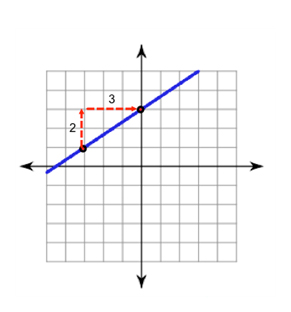
The slope of this line is \(\Large \frac{2}{3}\).
If we aren’t given a picture, we can still find the slope as long as we are given two points. You can always graph the two points and count like we did above, but there is a much quicker way!
\(slope = \Large \frac{{rise}}{{run}} = \Large \frac{{{y_2} - y{}_1}}{{{x_2} - {x_1}}}\)
Example 2:
Find the slope between the points (3, -2) & (5, -7).
First, label your points.
\((3, - 2)(5, - 7)\)
\(({x_1},{y_1})({x_2},{y_2})\)
Then, plug them in.
\(\Large \frac{{{y_2} - y{}_1}}{{{x_2} - {x_1}}} = \Large \frac{{( - 7) - ( - 2)}}{{5 - 3}} = \Large \frac{{ - 5}}{2}\)
The slope between the two points is \(\Large \frac{{ - 5}}{2}\).
Below you can download some free math worksheets and practice.
Find the slope of each line.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
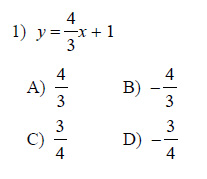
Watch below how to solve this example:
Find the slope of each line.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
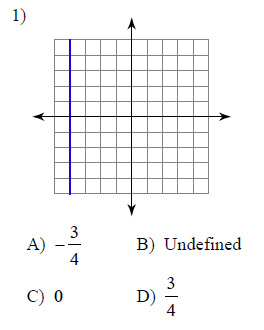
Watch below how to solve this example:
Find the slope of a line perpendicular to each given line.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
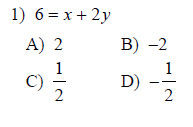
Watch below how to solve this example:


