Graphing absolute value equations
The graph of an absolute value equation will be interesting because of the unique nature of absolute value. Absolute Value is never negative. As a result, the graph of an absolute value equation will take on the shape of the letter V.
There is an easy procedure you can follow to graph absolute value equations:
- Plot the value of x such that the expression inside the absolute value bars is 0.
- Plot one x value less than that value.
- Plot one x value greater than that value.
- Connect the dots.
By strategically choosing the x value in the first step, we will secure the vertex of the graph, and by plotting one single point less than, and one point greater than that value, we will generate the x shape easily. Let’s take a look at an example:
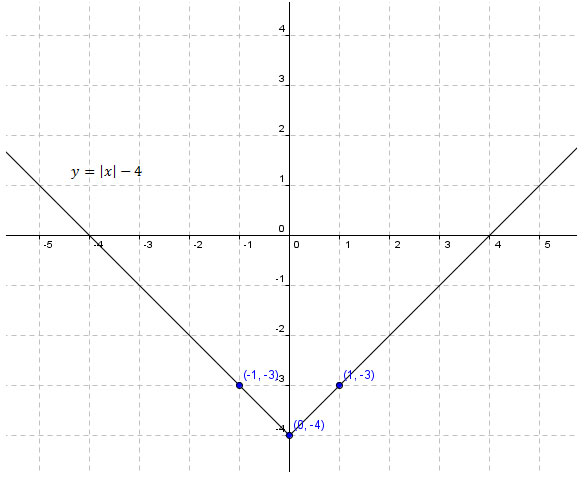
Example: Graph the equation y=|x|−4
Solution: We make a table of values. Following the procedure from above, we first plot that value of x that would make |x|=0. In this case, the value is x=0.
| x | y=|x|−4 |
| 0 | -4 |
Next we want to plot a single value of x less than 0, and a value of x greater than 0. We choose −1 and 1.
| x | y=|x|−4 |
| -1 | -3 |
| 0 | -4 |
| 1 | -3 |
Now it’s as easy as plotting the points and connecting the dots, remembering that the shape of the graph of an absolute value equation is always the shape of V. The graph is below.
Now let’s try one more example.
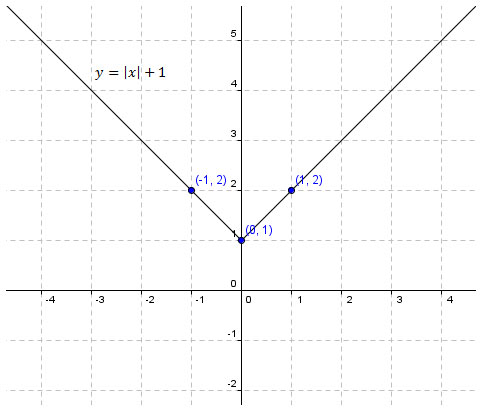
Example: Graph the equation y=|x|+1
Solution: Again, we plot the value of x such that |x|=0. That is x=0. Then we plot x=−1 and x=1, that we have one value less than 0, and one value greater than 0.
| x | y=|x|+1 |
| -1 | 2 |
| 0 | 1 |
| 1 | 2 |
Here is the graph:
Below you can download some free math worksheets and practice.
Graph each equation.
This free worksheet contains 10 assignments each with 24 questions with answers.
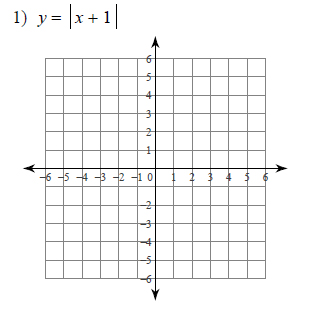
Example of one question:

Watch below how to solve this example:
Graph each equation.
This free worksheet contains 10 assignments each with 24 questions with answers.
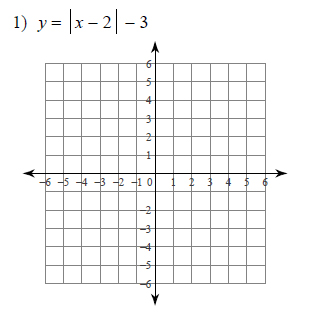
Example of one question:
Watch below how to solve this example:
Graph each equation.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch below how to solve this example:


