Dividing
Sometimes in mathematics there exist conventions that have lasted throughout the years. In the day and age of the super-powered calculators, these conventions do not always make sense anymore. But we continue to use them anyway. One of those conventions is that we must always rationalize the denominator in a radical expression. You have most likely already rationalized denominators in simple radical expressions such as
\(\Large \frac{2}{{\sqrt 3 }}\)
The way you rationalize the denominator in the above expression is by multiplying the expression by a fancy form of the number 1 that eliminates the radical in the denominator. In this case, we would multiply by \(\Large \frac{{\sqrt 3 }}{{\sqrt 3 }}\). Let’s see what happens when we do that. We have
\(\Large \frac{2}{{\sqrt 3 }} = \Large \frac{2}{{\sqrt 3 }} \cdot \Large \frac{{\sqrt 3 }}{{\sqrt 3 }}\)
\( = \Large \frac{{2\sqrt 3 }}{3}\)
And so we have rationalized the denominator. Note that a radical still remains in the expression. There’s nothing we can do about that. Now when dealing with more complicated expressions involving radicals, we employ what is known as the conjugate.
Definition: If \(a\sqrt b + c\sqrt d \) is a radical expression, then the conjugate is \(a\sqrt b - c\sqrt d \). The converse of this definition is also true.
Let’s look at an example of using the conjugate to rationalize the denominator. Simplify the expression
\(\Large \frac{4}{{5\sqrt 3 + 2}}\)
Here we will multiply both the numerator and denominator by the conjugate of the denominator, which is \(5\sqrt 3 - 2\). We can do this because we are in effect multiplying the expression by 1, which changes nothing. We have
\(\Large \frac{4}{{5\sqrt 3 + 2}} = \Large \frac{4}{{5\sqrt 3 + 2}} \cdot \Large \frac{{5\sqrt 3 - 2}}{{5\sqrt 3 - 2}}\)
\( = \Large \frac{{20\sqrt 3 - 8}}{{25 \cdot 3 - 10\sqrt 3 + 10\sqrt 3 - 4}}\), remembering to FOIL here
\( = \Large \frac{{20\sqrt 3 - 8}}{{71}}\)
Look what happened when we multiplied the denominator by the conjugate. The radical disappeared, and the denominator was rationalized. We must be careful and remember to FOIL in the second step. Let’s try one more example. Simplify the expression
\(\Large \frac{5}{{\sqrt 5 + 3\sqrt 3 }}\)
Again we will multiply both numerator and denominator by the conjugate of the denominator. In this case, we are multiplying both numerator and denominator by \(\sqrt 5 - 3\sqrt 3 \). We have
\(\Large \frac{5}{{\sqrt 5 + 3\sqrt 3 }} = \Large \frac{5}{{\sqrt 5 + 3\sqrt 3 }} \cdot \Large \frac{{\sqrt 5 - 3\sqrt 3 }}{{\sqrt 5 - 3\sqrt 3 }}\)
\( = \Large \frac{{5\sqrt 5 - 15\sqrt 3 }}{{5 - 3\sqrt {15} + 3\sqrt {15} - 9 \cdot 3}}\), remembering to FOIL here
\( = \Large \frac{{5\sqrt 5 - 15\sqrt 3 }}{{ - 22}}\)
\( = \Large \frac{{ - 5\sqrt 5 + 15\sqrt 3 }}{{22}}\)
Below you can download some free math worksheets and practice.
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
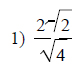
Watch below how to solve this example:
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
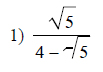
Watch below how to solve this example:
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
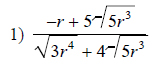
Watch below how to solve this example:


