The Midpoint Formula
If you wanted to find the point exactly in the middle of two numbers, what could you do? Of course, we could write out all the numbers and count to find the middle but there is a much easier and quicker way. We could always just take the average of the two numbers.
Example 1:
What would be the midpoint between 53 and 92?
Add the numbers:
\({\text{53 }} + {\text{ 92 }} = {\text{ 145}}\)
Divide by 2:
\({\text{145}} \div {\text{2 }} = {\text{ 72}}.{\text{5}}\)
So, 72.5 is the point directly in the middle of 53 and 92.
This is exactly what the midpoint formula does, except when you have a coordinate point, you have an x and a y, so you have to do this twice.
Midpoint = \((\Large \frac{{{x_2} + {x_1}}}{2},\Large \frac{{{y_2} + {y_1}}}{2})\)
The little “ones” and “twos” don’t matter too much since we are adding. The order won’t make a difference.
Example 2:
Find the midpoint between (3, -9) & (-2, 1)
\((\Large \frac{{{x_2} + {x_1}}}{2},\Large \frac{{{y_2} + {y_1}}}{2})\)
\((\Large \frac{{ - 2 + 3}}{2},\Large \frac{{1 + ( - 9)}}{2})\)
\((\Large \frac{1}{2},\Large \frac{{ - 8}}{2})\)
\((\Large \frac{1}{2}, - 4)\)
\((\Large \frac{1}{2}, - 4)\) is the midpoint between (3, -9) & (-2, 1).
Example 3:
Find the midpoint of the segment with the endpoints (5.1, 9) & (11.5, -7.8)
This is the same type of question, just be very careful with your simplifying. Don’t be scared of decimals!
\((\Large \frac{{{x_2} + {x_1}}}{2},\Large \frac{{{y_2} + {y_1}}}{2})\)
\((\Large \frac{{11.5 + 5.1}}{2},\Large \frac{{ - 7.8 + 9}}{2})\)
\((\Large \frac{{16.6}}{2},\Large \frac{{1.2}}{2})\)
\((8.3,0.6)\)
Answer: \((8.3,0.6)\)
There is a tougher type of question that uses the midpoint formula as well. If you are given the midpoint and only one endpoint and need to find the other endpoint, start with plugging in your values. We have to use the formula backwards.
Example 4:
Find the other endpoint of the segment with a midpoint of (3,4) and one endpoint of (-2,8).
Midpoint = \((\Large \frac{{{x_2} + {x_1}}}{2},\Large \frac{{{y_2} + {y_1}}}{2})\)
\((3,4) = (\Large \frac{{ - 2 + {x_1}}}{2},\Large \frac{{8 + {y_1}}}{2})\)
Now, split the x and the y and solve one at a time.
\(3 = \Large \frac{{ - 2 + {x_1}}}{2}\) Multiply both sides by 2. \(4 = \Large \frac{{8 + {y_1}}}{2}\)
\(6 = - 2 + {x_1}\) Move the constant to the other side. \(8 = 8 + {y_1}\)
\(8 = {x_1}\) \(0 = {y_1}\)
The other endpoint is (8,0).
Below you can download some free math worksheets and practice.
Find the midpoint of each line segment.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
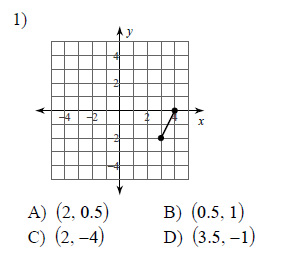
Watch below how to solve this example:
Find the midpoint of the line segment with the given endpoints.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:

Watch below how to solve this example:
Find the other endpoint of the line segment with the given endpoint and midpoint.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
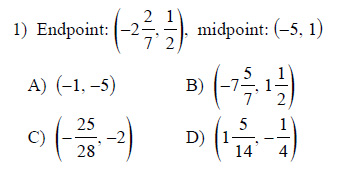
Watch below how to solve this example:


