Writing linear equations
There are two ways of using information to write the equation of a line. Both work equally as well, and unless are you asked to use a specific method, you can use whichever one makes more sense to you.
Method One:Slope-Intercept Form (\(y = mx + b\)) and solving for “b”.
Example 1:
Write the equation of the line with a slope of \(\Large \frac{9}{4}\) and goes through the point (4,5).
We want to get our equation in the form \(y = mx + b\). “m” stands for slope, so we have that part already! Since they also gave us a point, we can use these numbers and plug them in for x and y.
\(m = \Large \frac{9}{4}\) \(x = 4\) \(y = 5\)
\(y = mx + b\)
\({\text{5 }} = \Large \frac{9}{4}\left( {\text{4}} \right){\text{ }} + b\)
Simplify and solve for b.
\({\text{5 }} = {\text{ 9 }} + b\)
\( - {\text{4 }} = b\)
Now, plug “m” and “b” into your slope-intercept form
Answer: \(y = \Large \frac{9}{4}x--{\text{ 4}}\)
Method Two:Point-Slope Form
This way might be a little less confusing, but you have to remember a formula in order to use this method.
Point-Slope Form ►\((y - {y_1}) = m(x - {x_1})\)
Example 2:
Write the equation of a line with a slope of \(\Large \frac{5}{3}\) and goes through point (3,1)
We don’t have to worry about “b” in this method, so we already have all the parts that we need!
m = \(\Large \frac{5}{3}\) \({x_1} = 3\) \({y_1} = 1\)
\((y - {y_1}) = m(x - {x_1})\) Plug in values.
\((y - 1) = {\Large \frac{5}{3}}(x - 3)\) Distributive.
\(y - 1 = {\Large \frac{5}{3}x} - 5\) Add 1 to both sides.
Answer: \(y = {\Large \frac{5}{3}x} - 4\)
You can also figure out the equation of a line if you are only given 2 points. There is one extra step and then you can choose one of the above methods to complete it. Here’s an example:
Example 3:
Write the equation of a line that passes through points (4, -2) & (-6, 0)
It doesn’t matter which method we would like to use, for both of them we first need a slope! You can use both points to find the slope.
Slope = \({\Large \frac{{{y_2} - {y_1}}}{{{x_2} - x}}_1}\)
Let’s label our points:
\((4, - 2)( - 6,0)\)
\(({x_1},{y_1})({x_2},{y_2})\)
Now, plug them in.
\({\Large \frac{{{y_2} - {y_1}}}{{{x_2} - x}}_1} = \Large \frac{{0 - ( - 2)}}{{ - 6 - 4}} = \Large \frac{2}{{ - 10}} = - \Large \frac{1}{5}\)
So, the slope is
\( - \Large \frac{1}{5}\)
We will finish this problem using both methods, so you can decide which way you like best.
Slope-Intercept Method
Choose one of the points that we started with. (-6,0)
\(m = - \Large \frac{1}{5}\) \(x = - 6\) \(y = 0\)
\(y = mx + b\)
\(0 = - {\Large \frac{1}{5}}( - 6) + b\)
\(0 = {\Large \frac{6}{5}} + b\)
\( - \Large \frac{6}{5} = b\)
Answer: \(y = - \Large \frac{1}{5}x - \Large \frac{6}{5}\)
Point-Slope Method
\(m = - \Large \frac{1}{5}\) \({x_1} = - 6\) \({y_1} = 0\)
\((y - {y_1}) = m(x - {x_1})\)
\((y - 0) = - \Large \frac{1}{5}(x + 6)\)
\(y = - \Large \frac{1}{5}x - \Large \frac{6}{5}\)
Below you can download some free math worksheets and practice.
Write the slope-intercept form of the equation of each line given the slope and y-intercept.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:

Watch below how to solve this example:
Write the slope-intercept form of the equation of the line through the given point with the given slope.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
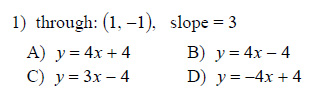
Watch below how to solve this example:
Write the standard form of the equation of the line described.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
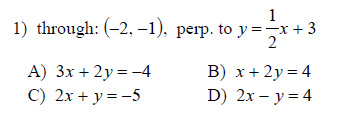
Watch below how to solve this example:


