Markup, discount, and tax
A lot of “real-life” math deals with percents and money. You will need to know how to figure out the price of something in a store after a discount. You will also need to know how to add tax to your items to make sure you brought enough money! If you do these problems enough, you can find shortcuts or “tricks” and use mental math to estimate but there is also a fail-proof procedure that will get you the exact result every time. Here it is:
This handy proportion can solve any percent problem. Let me explain how it works.
Example 1:
Let’s start off with a basic percent problem.
What is 12% of 155?
The percent always goes over the 100. The 155 is going to be our “OF” and we are looking for our “IS”. So the proportion will look like this:
\(\frac{x}{{155}} = \frac{{12}}{{100}}\) Now, cross multiply.\(x \bullet 100 = 12 \bullet 155\)
\(100x = 1860\)
\(x = 18.6\)
18.6 is 12% of 155.
Example 2:
Let’s try another.
9 is what percent of 215?
9 will be our “IS”, 215 is our “OF” and we are looking for our percent.
\(\frac{9}{{215}} = \frac{x}{{100}}\)
\(9 \bullet 100 = x \bullet 215\)
\(900 = 215x\)
\(x = 4.19\)
Now let’s apply this to shopping and figuring out discounts and taxes. Discounts are subtracted off the price and tax is added on.
Example 3:
Original price of a parrot is $194.50
There is a 5% discount.
Tax is 3%.
Let’s first figure this out: What is 5% of 194.50?
\(\frac{x}{{194.50}} = \frac{5}{{100}}\)
\(x \bullet 100 = 5 \bullet 194.50\)
\(100x = 972.50\)
\(x = 9.725\)
Let’s subtract this off the original price.
$194.50
- 9.725 5% Discount
184.775
Next, let’s figure this out: What is 3% of 184.775?
\(\frac{x}{{184.775}} = \frac{3}{{100}}\)
\(x \bullet 100 = 3 \bullet 184.775\)
\(100x = 554.325\)
\(x = 5.54325\)
Let’s add this to the discounted price.
184.775
+ 5.54325 3% Tax
190.31825
Let’s round off to two decimal places since we are dealing with money.
Our parrot will cost $190.32
So this seems like a lot of work for one problem. There is a shorter way! You can also change the percents to decimals and use multiplication. Let’s try one that way.
Example 4:
Original price of a hat is $28.50
There is a discount of 40%.
Tax is 5%.
When you change a percent to a decimal you divide by 100 or just simply move the decimal to the left 2 places.
40% = .40
5% = .05
It actually won’t matter is you subtract the discount first or add the tax first. Let’s deal with the discount first.
Now, using this new price, let’s add the tax.
Below you can download some free math worksheets and practice.
Find the selling price of each item.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
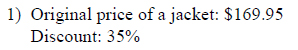
Watch below how to solve this example:
Find the selling price of each item.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
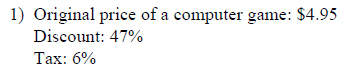
Watch below how to solve this example:
Find the selling price of each item.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
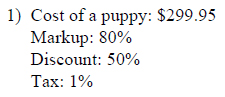
Watch below how to solve this example:


