Simplifying single radicals
Using an important property of radicals allows us to simplify radicals as much as possible. Let’s state the property below.
Definition: If a and b are any numbers, then the following property holds:
\(\sqrt a \cdot \sqrt b = \sqrt {ab} \)
We can use this property and prime factorization to simplify complicated looking radicals. Let’s try an example.
Simplify \(10\sqrt {343{x^2}} \).
Let’s look at the prime factorization of the number under the radical, 343. We want to see if there are any perfect squares embedded in 343. We have
\(343 = 7*49\)
\( = 7*{7^2}\)
There is a perfect square, 49, embedded within 343. Now we will rewrite 343 in a convenient way to simplify. We have
\(10\sqrt {343{x^2}} = 10\sqrt {7*{7^2}*{x^2}} \)
Now implement the property of radicals that we discussed above and simplify each individual radical one at a time.
\(10\sqrt {343{x^2}} = 10\sqrt {7*{7^2}*{x^2}} \)
\( = 10*\sqrt 7 *\sqrt {{7^2}} *\sqrt {{x^2}} \)
\( = 10*\sqrt 7 *7*\left| x \right|,\), don't forget that \(\sqrt {{x^2}} = |x|\)
So we have simplified a radical. \(10\sqrt {343{x^2}} = 70\left| x \right|\sqrt 7 \). Why don’t we do another example?
Simplify \(2\sqrt {216{n^5}} \). Again we want to break down 216 into its prime factorizations to see if there are any perfect squares lurking inside. We have
\(216 = 2*108\)
\( = 2*2*54\)
\( = {2^2}*54\)
\( = {2^2}*9*6\)
\( = {2^2}*{3^2}*6\)
In fact, there are two perfect squares embedded within 216. Let’s rewrite our radical expression and finish simplifying:
\(2\sqrt {216{n^5}} = 2\sqrt {{2^2}*{3^2}*6*{n^2}*{n^2}*n} \)
\( = 2*\sqrt {{2^2}} *\sqrt {{3^2}} *\sqrt 6 *\sqrt {{n^2}} *\sqrt {{n^2}} *\sqrt n \), from the property of radicals
\( = 2*2*3*\sqrt 6 *\left| n \right|*\left| n \right|*\sqrt n \)
\( = 12*\sqrt 6 *\left| {{n^2}} \right|*\sqrt n \)
\( = 12{n^2}\sqrt {6n} \), disregard the absolute value bars since \({n^2}\) is always positive
So \(2\sqrt {216{n^5}} = 12{n^2}\sqrt {6n} \).
As you practice more with simplifying radicals, the procedure becomes so fast that you’ll be doing most of it in your head without writing the intermediate simplifying steps. Good luck!
Below you can download some free math worksheets and practice.
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:
Simplify. Use absolute value signs when necessary.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
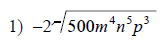
Watch below how to solve this example:


