Circle constructions
To construct a circle, you will need a compass and a ruler or straightedge.
A chord is a line segment that fits inside the circle.
A perpendicular bisector is a line that divides another line into two equal parts at a right angle.
Here are the steps to find the center of a circle.
- Draw two separate chords inside the circle. It works best if they are not parallel.
- You must construct the perpendicular bisector of both of these lines. Set the width of the compass to a little more than half of the total chord (the width doesn’t matter so much, as long as it does not change during this step)
- Put the point of the compass on one endpoint of the line and use the pencil side to draw a small arc on the top and the bottom of the line.
- Without changing the width, repeat this step using the other endpoint of the line.
- The arcs should intersect at a point above and a point below the line. Using the ruler, connect these points with a straight line. This is your perpendicular bisector.
- Repeat steps 2-5 for the other chord as well.
- The point where these two perpendicular bisectors intersect is the center of the circle.
To circumscribe is when you draw a circle around a figure enclosing it while touching all sides of vertices of the figure.
Here are the steps to circumscribe a circle around a rectangle.
- Find the center of the rectangle by drawing both diagonals. The place where they intersect is the center.
- This is also the center of your circle. Put the point of the compass on this center point and the pencil part on one of the sides of the rectangle.
- Being careful not to change the width of the compass, draw a circle. It should touch all sides of the rectangle and completely enclose it inside the circle.
Inscribing is when you draw a circle inside a figure so that it touches all the sides or vertices of the figure. To inscribe a circle inside a triangle, you must know how to find the incenter.
The incenter is where all three angle bisectors of the triangle intersect.
An angle bisector is a line that cuts an angle in half. It divides the angle into two congruent angles.
Here are the steps to inscribing a circle inside a triangle.
- Place the point of the compass at on of the vertices of the triangle. Set the width of the compass to about half of one of the sides (the width actually doesn’t matter, as long as it does not change during the next couple of steps)
- Draw a small arc through the two sides of the angle. Remember to not change the width of the compass.
- Also without changing the width, place the point of the compass at the intersection of the arc and the side of the angle. Draw a new arc in the interior of the triangle. Repeat this for the other side of the angle.
- The arcs should intersect in the interior of the triangle. Using a ruler or straightedge, connect the intersection of the interior arcs and the vertex of the angle. This is your angle bisector.
- Do this again for a different vertex.
- You can construct the third angle bisector for added accuracy, but you only need two to find the incenter.
- The incenter is the spot where the angle bisectors intersect.
- Place the point of the compass on the incenter and the pencil side on one of the sides of the triangle.
- Carefully, use the compass to draw a circle inside the triangle. The circle should fit snugly inside the triangle while touching all three sides.
Locate the center of each circle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:

Watch below how to solve this example:
Circumscribe a circle about each rectangle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
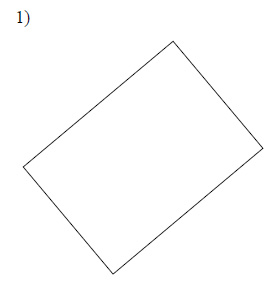
Watch below how to solve this example:
Inscribe a circle in each triangle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
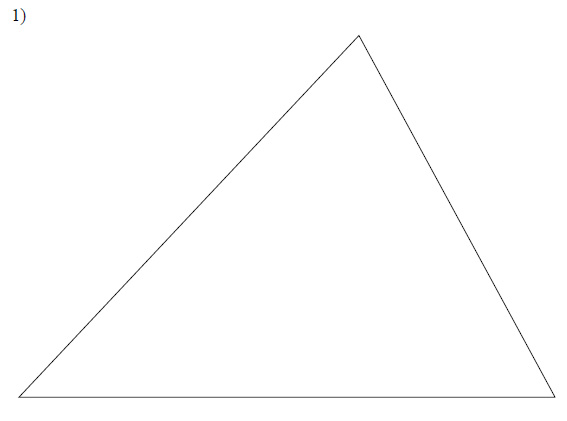
Watch below how to solve this example:


