Sets of numbers
In the world of mathematics we have categorized all the numbers that exist into certain sets. Let’s describe the certain sets that exist as well as their properties:
The Set of Natural Numbers
Definition: The set \(\mathbb{N}\) of natural numbers is defined by
\(\mathbb{N} = \left\{ {1,2,3, \ldots } \right\}\)
The set of natural numbers is often referred to as the set of counting numbers, because they are those numbers that we use to count. Notice the three dots in the set notation. That means that the set continues without end. Also notice that 0 is not included in the natural numbers.
The Set of Integers
Definition: The set \(\mathbb{Z}\) of integers is defined by
\(\mathbb{Z} = \left\{ { \ldots , - 3, - 2, - 1,0,1,2,3, \ldots } \right\}\)
The set of integers contains all whole numbers (including 0) and their opposites. Notice that the set of natural numbers is contained within the set of integers.
The Set of Rational Numbers
Definition: The set \(\mathbb{Q}\) of rational numbers is defined by
\(\mathbb{Q} = \large \left\{ {\frac{m}{n}:m,n{\text{ are integers}}} \right\}\)
Here is the set of rational numbers, all those numbers that can be expressed as a ratio of two integers. Furthermore, the set of rational numbers includes all those numbers whose decimal representation terminates or repeats.
The Set of Irrational Numbers
Definition: The set of Irrational Numbers is defined by those numbers whose decimal representations never terminates or repeats. Some famous irrational numbers include \(\pi \) and \(\sqrt 2 \). In fact, \(\sqrt n \) is irrational if \(n\) is not a perfect square.
Together all these sets combined make up the SET OF REAL NUMBERS.
Example: Name the set or sets to which 0 belongs.
Solution: By inspection we see that 0 is a member of the integers, the rational numbers (since \(\large \frac{0}{1} = 0\), and the real numbers.
Example: Name the set or sets to which \(\sqrt {82} \) belongs.
Solution: Since 82 is not a perfect square, \(\sqrt {82} \) is irrational. Therefore it cannot be rational, an integer, or a natural number. But it is a real number.
Below you can download some free math worksheets and practice.
Name the set or sets to which each number belongs.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch below how to solve this example:
Name the set or sets to which each number belongs.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
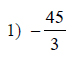
Watch below how to solve this example:
Name the set or sets to which each number belongs.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
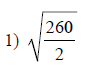
Watch below how to solve this example:


