Graphing
There are a few pieces of information that you have to put together in order to create a graph of a quadratic function. Before anything, though, we need to learn the standard form of a quadratic and this is it:
\(ax^2 + bx + c\)
a,b,and c are all numbers
For example, what are a,b, and c in the following expression?
\(2x^2 + 4x - 3\)
a = 2 b = 4 c = -3
Great! That’s the first step. Next little piece of info that you will need is that every time you graph a quadratic, it is going to look like a “u” shape, which is called a parabola. If your first number (your “a”) is positive then it will look like a smiley face parabola (opens up) and if “a” is negative, then your parabola will be a frowny face (opens down).
| \(x^2=\) |
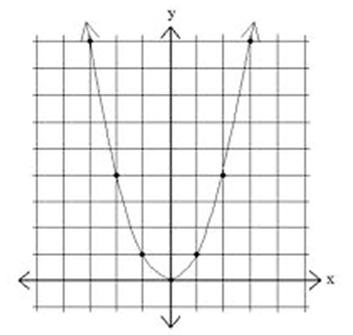 |
\(-x^2=\) |
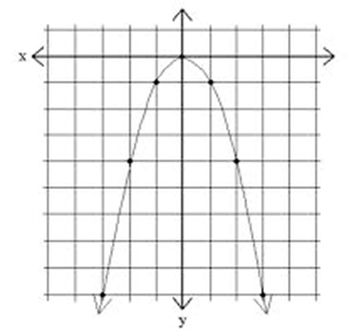 |
We are almost ready to graph. Two more pieces to go. The first one is something called the axis of symmetry. Symmetry means there is a line that exists that you can fold over to make the graph overlap itself. If you look at the two graphs above, can you see where that line might be? It’s right down the center at the y-axis on both graphs.
This line is going to help us graph. Here’s how you find it:
Axis of Symmetry (AOS) ► \(x=\frac{-b}{2a}\)
These are your same a and b as before. Let’s use our above example:
\(2x^2 + 4x - 3\)
a = 2 b = 4 c = -3
\(x=\frac{-b}{2a}=\frac{-4}{2(2)}=\frac{-4}{4}=-1\)
\(x=-1\)
Our AOS is x = -1. We can show this on the graph by drawing a dotted line at x = -1. Your AOS (in this chapter) will always be a vertical line.
Almost done! We need one more thing. It’s called the vertex, which is the highest or lowest point depending on whether the parabola opens up or opens down.
To find the vertex, take the value (the “x”) that you found for the AOS and plug it into the equation to find the “y”.
\(x=-1\)
\(y=2x^2 + 4x -3\)
\(y = 2(-1)^2 + 4(-1) - 3\)
\(y = -5\)
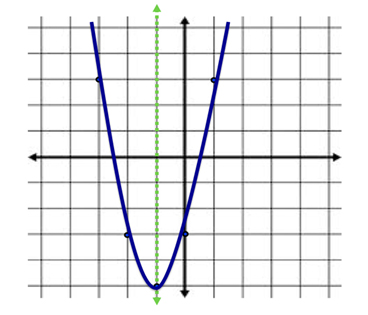
So, your vertex is at the point (-1,-5). If you want to sketch the graph, you now have enough information. If we want it to be very accurate, we need a few more points. Pick some before and after the AOS and plug into your equation.
| \(x\) | \(2x^2 + 4x - 3\) | \(y\) |
| -3 | \(2(-3)^2 + 4(-3) - 3\) | 3 |
| -2 | \(2(-2)^2 + 4(-2) - 3\) | -3 |
| -1 | \(2(-1)^2 + 4(-1) - 3\) | -5 |
| 0 | \(2(0)^2 + 4(0) - 3\) | -3 |
| 1 | \(2(1)^2 + 4(1) - 3\) | 3 |
Bellow you can download some free math worksheets and practice.
Sketch the graph of each function.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch below how to solve this example:
Sketch the graph of each function.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch below how to solve this example:
Sketch the graph of each function.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch below how to solve this example:


