Work word problems
Sometimes you will encounter a word problem that asks you to determine how long it would take two people working together to finish a job. Solving this type of problem requires a few steps of logic. Let’s jump straight to an example.
Example: Jennifer can mop a warehouse in 8.3 hours. Heather can mop the same warehouse in 11.2 hours. Find how long it would take them if they worked together.
Solution: We set up an equation to model Jen’s work. We know that Jen can mop a warehouse in 8.3 hours, which means
\(\Large \frac{{1{\text{Warehouse Mopped}}}}{{8.3{\text{ hours}}}} = 0.12{\text{Warehouse Mopped in }}1{\text{ hour}}\)
That is, Jen can mop 12 percent of the warehouse in one hour. We set up a similar equation for Heather. We know that Heather can mop the same warehouse in 11.2 hours, which means
\(\Large \frac{{1{\text{Warehouse Mopped}}}}{{11.2{\text{ hours}}}} = 0.09{\text{Warehouse Mopped in }}1{\text{ hour}}\)
That is, Heather can mop about 9 percent of the warehouse in one hour. Now we can find out how much of the warehouse they can mop together in one hour. We have
\(0.12\left( {for Jen} \right) + 0.09\left( {for Heather} \right) = 0.21\)
That is, together they can mop 21 percent of the warehouse in 1 hour. Let’s set up our final equation to model this word problem. We use a simple ratio:
\(\Large \frac{{1{\text{Warehouse Mopped}}}}{{x{\text{ hours}}}} = \Large \frac{{0.21{\text{Warehouse Mopped}}}}{{1{\text{ hour}}}}\)
Cross multiplying gives
\(x = \Large \frac{1}{{0.21}} = 4.76{\text{ hours}}\)
Another Example: Molly can clean an attic in 10.6 hours. Jasmine can clean the same attic in 15 hours. If they worked together how long would it take them?
\(\Large \frac{{1 Attic}}{{10.6 hours}} = 0.09 in one hour\)
For Jasmine, we have
\(\Large \frac{{1 Attic}}{{15 hours}} = 0.07 in one hour\)
Together, their labor yields
\(0.09 + 0.07 = 0.16 together in one hour\)
Then we use another ratio to solve the problem
\(\Large \frac{{1 Attic Cleaned}}{{x hours}} = \Large \frac{{0.16 Cleaned}}{{1 hour}}\)
Then, by cross multiplying,
\(x = \Large \frac{1}{{0.16}} = 6.25 hours\)
Below you can download some free math worksheets and practice.
Solve each question. Round your answer to the nearest hundredth.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:

Watch below how to solve this example:
Solve each question. Round your answer to the nearest hundredth.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
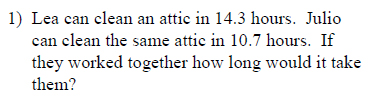
Watch below how to solve this example:
Solve each question. Round your answer to the nearest hundredth.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
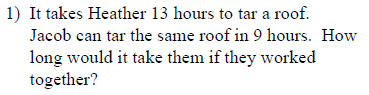
Watch below how to solve this example:


