Using equations of circles
Now that we know what the equation of a circle means, we can use it to identify the center and the radius and sketch the graph of the circle in the plane. But just for a refresher, let’s restate the definition of the equation of a circle.
DEFINITION: The equation of a circle with center \(\left( {h,k} \right)\) and radius \(r\) is given by
\({\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\)
Let’s implement this information now.
EXAMPLE: Identify the center and radius of the circle. Then sketch the graph of the circle.
\({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y + \frac{1}{2}} \right)^2} = 4\)
SOLUTION: We manipulate this equation slightly to get it exactly in the form above:
\({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y + \frac{1}{2}} \right)^2} = 4\)
\({\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - \left( { - \frac{1}{2}} \right)} \right)^2} = {2^2}\)
Now this equation is in the general form. From here we can conclude that
\({\text{Radius}} = 2\)
\({\text{Centeris}}\left( {\Large \frac{1}{2}, - \Large \frac{1}{2}} \right)\)
Here is the graph:
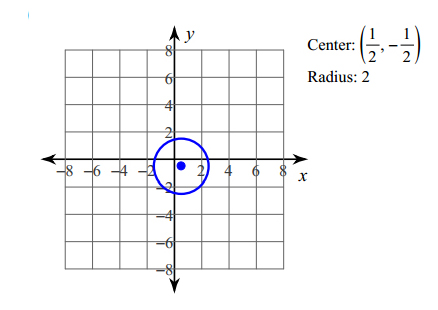
EXAMPLE: Identify the center and radius of the circle. Then sketch the graph of the circle.
\({\left( {x - 2} \right)^2} + {\left( {y - \frac{7}{2}} \right)^2} = 7\)
SOLUTION: Again we manipulate the equation into the general form. We have
\({\left( {x - 2} \right)^2} + {\left( {y - \frac{7}{2}} \right)^2} = 7\)
\({\left( {x - 2} \right)^2} + {\left( {y - \frac{7}{2}} \right)^2} = {\left( {\sqrt 7 } \right)^2}\)
Then the radius of the circle is \(\sqrt 7 \approx 2.6\), and the center is \(\left( {2,\frac{7}{2}} \right)\). The graph is below.
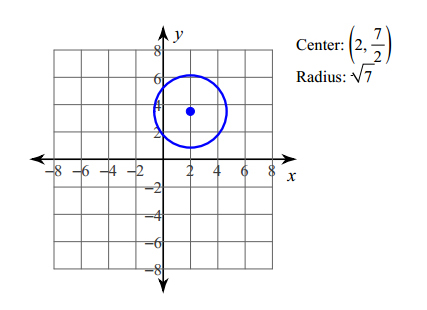
Below you can download some free math worksheets and practice.
Graph each equation.
This free worksheet contains 10 assignments each with 24 questions with answers.
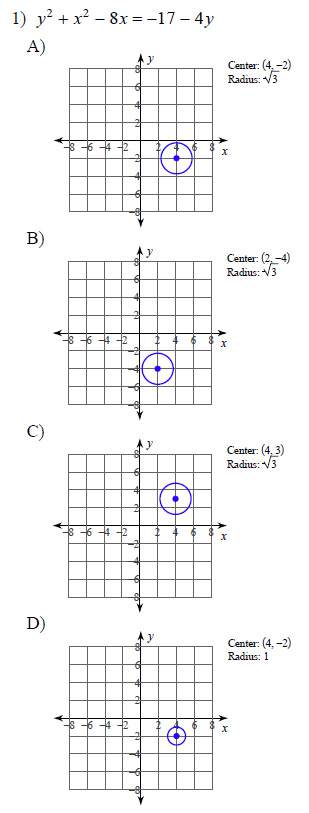
Example of one question:
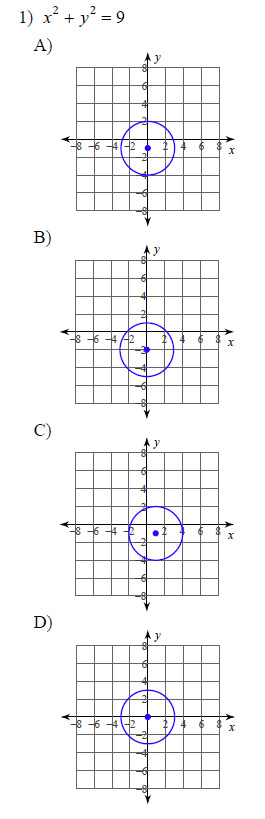
Watch bellow how to solve this example:
Identify the center and radius of each. Then sketch the graph.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
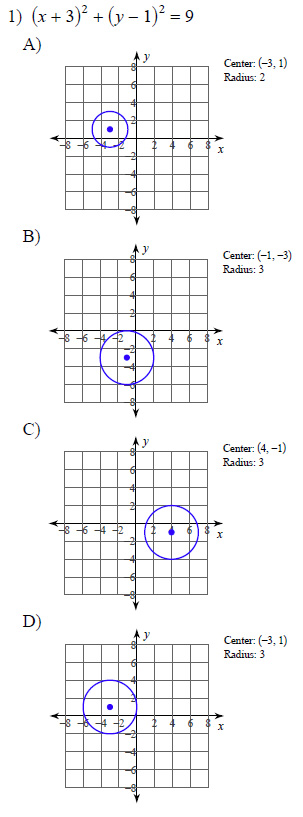
Watch bellow how to solve this example:
Identify the center and radius of each. Then sketch the graph.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch bellow how to solve this example:


