Medians
In Geoemetry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side.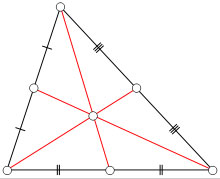
In the figure above, the medians are in red. Notice that each median bisects one side of the triangle, so that the two lengths on either side of the median are equal.
Example:
Find \(x\) if \(CY = \frac{1}{2}x - 1\) and \(CZ = \frac{{2x - 9}}{2}\)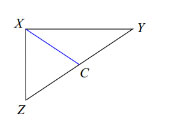
Solution: Here the median \(XC\) bisects the length \(ZY\), so that each of the two segments \(CZ\) and \(CY\) are equal to each other. Since \(CZ = CY\), we have
\(\frac{1}{2}x - 1 = \frac{{2x - 9}}{2}\)
Multiplying both sides by 2 gives us
Then solving for \(x\), we have
\(x = 7\)
So you see that the median can be useful for solving triangle problems.
Example: Find \(x\) if \(FS = x\) and \(FY = x + 3\)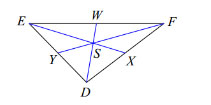
Solution: Here the median \(FY\) passes through the centroid of the triangle. By the property of the centroid, this will cut the median \(FY\) into two segments \(FS\) and \(SY\) whose lengths are in the ratio 2:1. That is, if \(FS = x\), we have that \(SY = \frac{1}{2}x\). Then the sum of \(FS\) and \(SY\) is \(FY\). That is,
\(x + \frac{1}{2}x = x + 3\)
Then by multiplying both sides by 2, we have
and solving for \(x\) gives us \(x = 6\).
Each figure shows a triangle with one or more of its medians.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
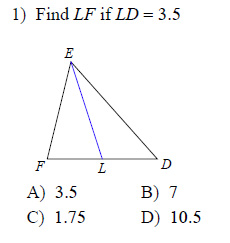
Watch below how to solve this example:
Each figure shows a triangle with one or more of its medians.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
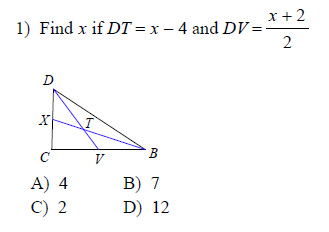
Watch below how to solve this example:
Each figure shows a triangle with one or more of its medians.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
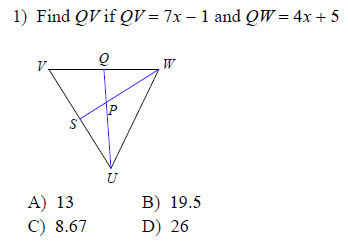
Watch below how to solve this example:


