Medians of a triangle constructions
The median of a triangle is the segment from the midpoint of one of the sides to the opposite vertex. There are three medians in a triangle.
To construct a median of a triangle, you will need a compass and a ruler or straightedge.
Here are the steps to constructing the median of a triangle.
Choose a side of the triangle. Place the point of the compass at one of the endpoints of that side. Set the width of the compass to a little more than half of the side (the width actually doesn’t matter, as long as it does not change during the next couple of steps).
- Draw a small arc above the line and a small arc below the line.
- Without changing the width, place the point of the compass at the other endpoint of the line and again draw a small arc above the line and a small arc below the line.
- The arcs should intersect above and below the line. Using a ruler or straightedge, connect the intersection of the arcs. This is the midpoint of the line.
- To draw the median, use your straightedge and connect this midpoint with the vertex across from it.
A triangle has three different medians. These lines will all meet together inside the triangle. Lines are called concurrent if they all intersect and the point of concurrency of the three medians is called a centroid. The purpose of a centroid is that it is the center of balance for the triangle.
Here are the steps to constructing the centroid of a triangle.
- Repeat the above steps and construct one of the medians of the triangle.
- Do this again for a different side.
- You can construct the third median for added accuracy, but you only need two to find the centroid.
- The centroid is the spot where the medians intersect.
Below you can download some free math worksheets and practice.
For each triangle, construct the median from vertex A.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
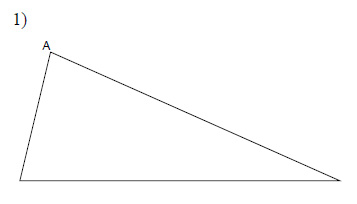
Watch below how to solve this example:
Locate the centroid of each triangle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
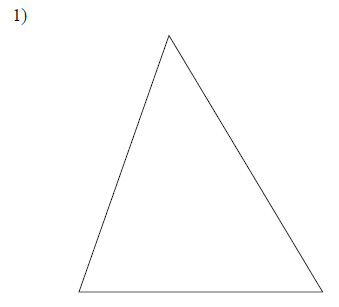
Watch below how to solve this example:
For each triangle, construct all three medians to show they are concurrent.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
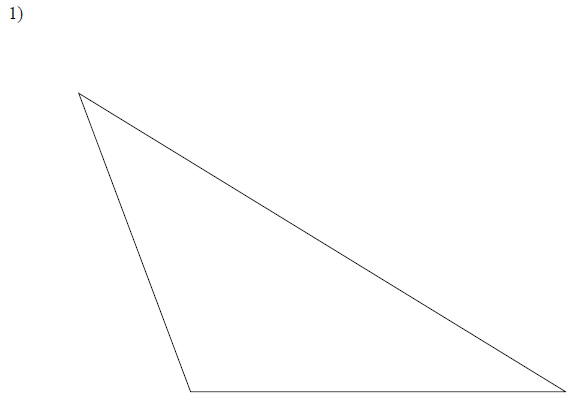
Watch below how to solve this example:


