The Distance Formula
If we have a straight line, it’s very easy to find out what the distance is from one point to the other. We count!
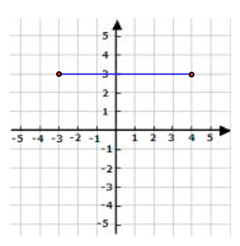
We can count the boxes and see that the line takes up 7 of them, so the distance of this line is 7.
Unfortunately, all lines aren’t straight. We need a way to figure out the distance if the line happens to be diagonal.
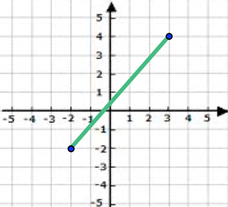
One thing we can do is draw in a right triangle and use Pythagorean’s Theorem. Do you remember that formula? It’s \({a^2} + {b^2} = {c^2}\). Let’s try that.
Example 1:
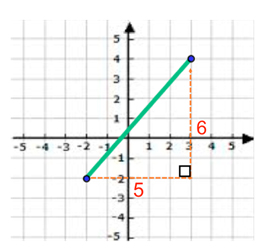
We can now count the boxes of the two legs of the triangle and use them in the formula.
\({a^2} + {b^2} = {c^2}\)
\({5^2} + {6^2} = {c^2}\)
\(25 + 36 = {c^2}\)
\(61 = {c^2}\)
\(\sqrt {61} = c\)
\(7.8 \approx c\)
There’s got to be an easier way! This would take a very long time if we had to draw a triangle every time we needed to find the distance between two points. Mathematicians have come up with a formula that does what we just did, without all the work. Here it is:
\(d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \)
Do you see Pythagorean’s Theorem hidden in there? Let’s try using this formula.
Example 2:
Find the distance between the points A(-3,2) & B(4,-1)
First, label the points:
\(( - 3,2)(4, - 1)\)
\(({x_1},{y_1})({x_2},{y_2})\)
Now, plug them in:
\(d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} \)
\(d = \sqrt {{{(4 - ( - 3))}^2} + {{( - 1 - 2)}^2}} \)
\(d = \sqrt {{{(7)}^2} + {{( - 3)}^2}} \)
\(d = \sqrt {49 + 9} \)
\(d = \sqrt {58} \)
\(d \approx 7.6\)
\(\overline {AB} \approx 7.6\)
A few things to be careful of when simplifying:
- When you subtract a negative number, it changes to addition!
- When you square a negative number, it always becomes positive!
- Your distance should never be a negative number!
Below you can download some free math worksheets and practice.
Find the distance between each pair of points. Round your answer to the nearest tenth, if necessary.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
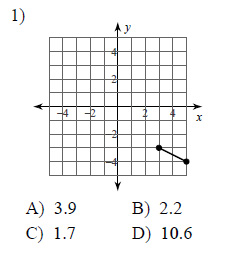
Watch below how to solve this example:
Find the distance between each pair of points. Round your answer to the nearest tenth, if necessary.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
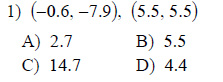
Watch below how to solve this example:
Find the distance between each pair of points.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
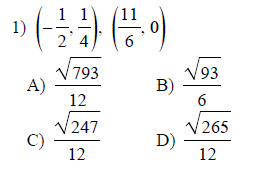
Watch below how to solve this example:


