Graphing linear equations
We can easily graph any equation given in slope-intercept form.
DEFINITION: The slope-intercept form of a linear equation is given by
\(y = mx + b\)
where \(m\) is the slope of the line, and is the point where the line intercepts the \(y\)-axis (that is, \(b\) is the \(y\)-intercept).
Essentially, when you have a line in slope intercept form, the slope and a point are given to you straight away. You only need to plot the given point, and use the slope to plot another point. Then connect the dots. It’s that easy.
EXAMPLE: Sketch the graph of the line whose equation \(y = - {\Large \frac{1}{2}x} + 2\)
SOLUTION: Here we have an equation in slope intercept form, with \(m = - \Large \frac{1}{2}\) (that is, the slope of the line is \( - \Large \frac{1}{2}\)), and \(b = 2\) (that is, the \(y\)-intercept is 2). We begin by plotting the \(y\)-intercept:
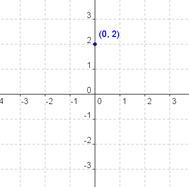
Next, we use the slope to find our next point. The slope is \( - \Large \frac{1}{2}\), so we move one unit down (because of the negative slope) and two units to the right. This puts us at the point \(\left( {2,1} \right)\). Then we connect the dots.
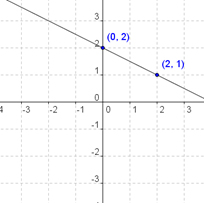
EXAMPLE: Sketch the graph of the line whose equation is \(y = - {\Large \frac{7}{5}x} - 5\).
SOLUTION: Here we are given another line in slope-intercept form, with \(m = - \Large \frac{7}{5}\), and \(b = - 5\). Then the first point we plot is the \(y\)-intercept at \( - 5\):
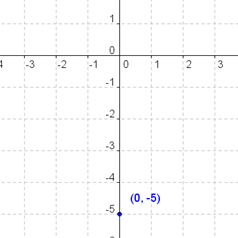
Then since the slope is \( - \Large \frac{7}{5}\), we move down 7 units, and right 5 units. Then connect the dots, and we’re finished!
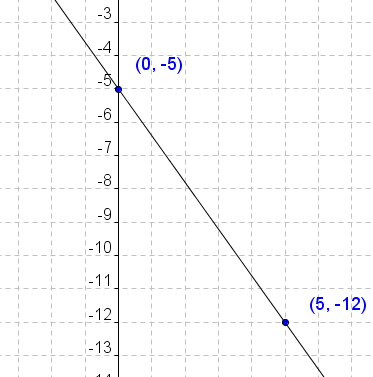
Below you can download some free math worksheets and practice.
Sketch the graph of each line.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
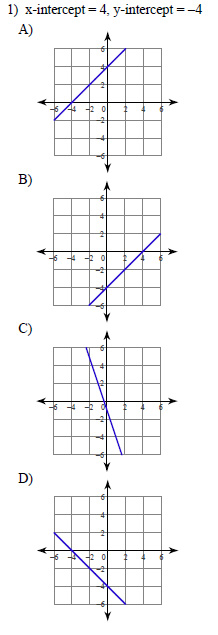
Watch below how to solve this example:
Sketch the graph of each line.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
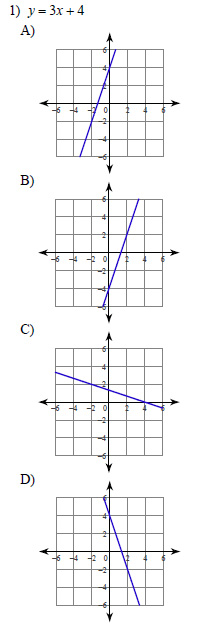
Watch below how to solve this example:
Sketch the graph of each line.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
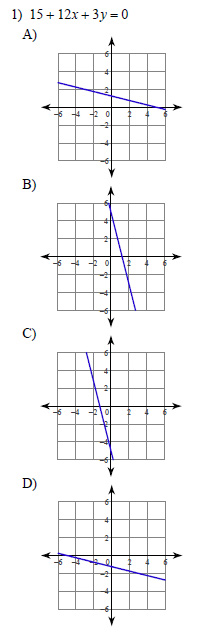
Watch below how to solve this example:


