Triangles and Congruence
Triangles have 6 parts. Can you guess them? We all know they have three sides, but don’t forget about their three angles as well! When triangles are congruent it means that they have the same size sides and the same angle measures. All six parts of one triangle will match all six parts of the congruent triangle.
The parts that match are called corresponding and they will be marked the same. Let’s take a look at an example:
Example 1:
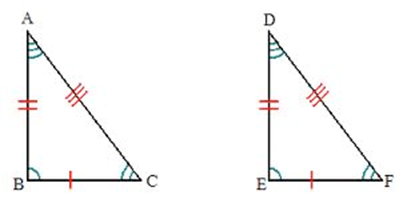
Let’s match up our corresponding angles first.
\(\angle {\text{A }}\& \angle {\text{D}}\) both have three curves in their angle, which mean they are corresponding and have the same measure. So our corresponding angles are:
\(\angle {\text{A }}\& \angle {\text{D}}\)
\(\angle {\text{B }}\& \angle {\text{E}}\)
\(\angle {\text{C}}\& \angle {\text{F}}\)
Now, let’s get to the sides.
\(\overline {AC} \& \overline {DF} \) both have three lines slashed through them to show that they are corresponding and are the same size. So our corresponding sides are:
\(\overline {AC} \& \overline {DF} \)
\(\overline {AB} \& \overline {DE} \)
\(\overline {BC} \& \overline {EF} \)
We can now come up with what is called a congruence statement. Since all 6 parts of the triangle are congruent, we can say that both triangles are exactly the same. You have to be careful when writing the congruence statement because the letters of one triangle have to match with the corresponding letters of the other triangle. For example, if we name the first triangle in our problem \(\Delta ABC\), we have to name the other triangle \(\Delta DEF\) by matching the corresponding angles and putting them in the same order. Our congruence statement would look like this:
\(\Delta ABC \cong \Delta DEF\)
We can also work with this statement backwards. Meaning, if we start with a congruence statement, we are able to tell which parts of the triangle are corresponding and therefore congruent.
Example 2:
\(\Delta JKL \cong \Delta XYZ\)
The corresponding angles must go in the same order, so our corresponding, congruent angles are:
\(\angle J \cong \angle X\)
\(\angle K \cong \angle Y\)
\(\angle L \cong \angle Z\)
The congruent sides go in order as well.
\(\overline {JK} \cong \overline {XY} \) (first & second letters)
\(\overline {KL} \cong \overline {YZ} \) (second & third letters)
\(\overline {JL} \cong \overline {XZ} \) (first & third letters)
** The order of the letters when naming the lines doesn’t make a difference. \(\overline {KL} \) is the same thing as \(\overline {LK} \).
Example 3:
Match the congruence statement to the correct pair of triangles (the corresponding parts must be labeled the same).
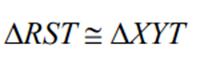
You can tell by the congruence statement that \(\angle R\& \angle X\) are corresponding angles and should be marked the same.
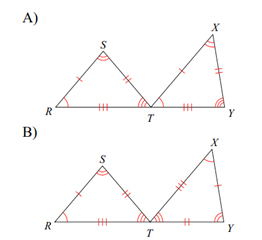
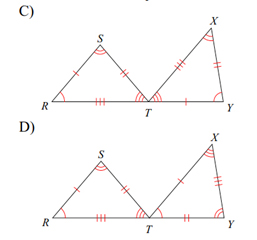
Answer B is the only pair of triangles where \(\angle R\& \angle X\) are marked the same. If you check the rest of the corresponding parts, they will match too!
Below you can download some free math worksheets and practice.
Complete each congruence statement by naming the corresponding angle or side.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
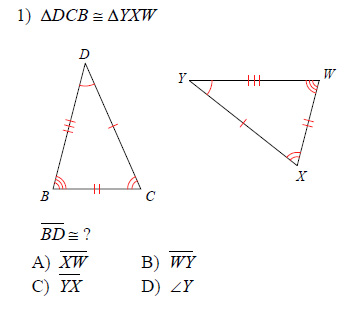
Watch below how to solve this example:
Mark the angles and sides of each pair of triangles to indicate that they are congruent.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
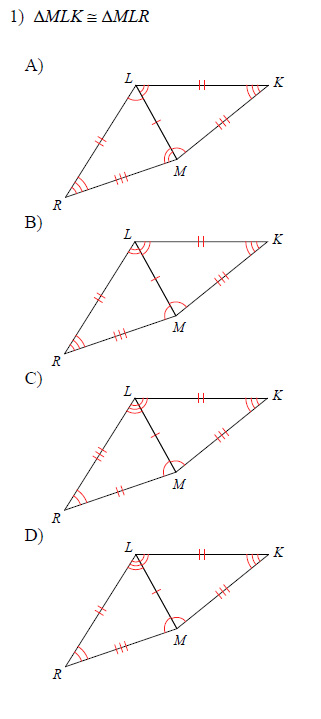
Watch below how to solve this example:
Write a statement that indicates that the triangles in each pair are congruent.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
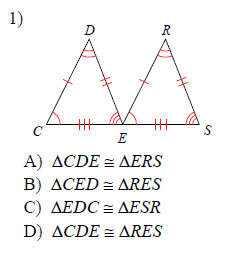
Watch below how to solve this example:


