Segment measures
We can recall certain theorems from geometry to help us find the length of segments in circles. We begin by stating an important theorem.
THEOREM: If two secant segments intersect outside a circle, then the product of the secant segment with its external portion equals the product of the other secant segment with its external portion.
Let’s use this theorem to solve some problems.
Example: Find RS
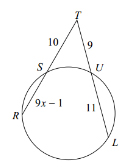
Solution: Here we have two secant segments, \(\overline {RT} \) and \(\overline {LT} \), intersecting outside a circle. Then, by our theorem, the product of the secant segment \(\overline {RT} \) with its external portion \(\overline {ST} \) equals the product of the other secant segment \(\overline {LT} \) with its external portion \(\overline {UT} \). That is,
\(\overline {RT} \cdot \overline {ST} = \overline {LT} \cdot \overline {UT} \)
Substituting, we have
\(\left[ {\left( {9x - 1} \right) + 10} \right] \cdot 10 = \left[ {11 + 9} \right] \cdot 9\)
\(\left( {9x + 9} \right)\left( {10} \right) = \left( {20} \right)\left( 9 \right)\)
\(90x + 90 = 180\)
\(90x = 90\)
\(x = 1\)
Now the length of \(\overline {RS} \) is \(9x - 1\), and with \(x = 1\), we have
\(\overline {RS} = 9\left( 1 \right) - 1 = 8\)
So we have put our theorem to good use to solve a problem.
Now let’s use another theorem to solve another problem.
THEOREM: If two chords intersect inside a circle, then the product of the segments of one chord equals the product of the segments of the other chord.
Example: Find JE
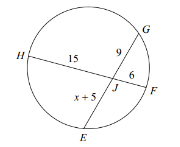
SOLUTION: Here we have two chords intersecting inside a circle. Then, by our theorem, the product of the segments of one chord equals the product of the segments of the other chord. That is,
\(\overline {HJ} \cdot \overline {JF} = \overline {EJ} \cdot \overline {JG} \)
Substituting gives us
\(15 \cdot 6 = \left( {x + 5} \right) \cdot 9\)
\(90 = \left( {x + 5} \right) \cdot 9\)
\(10 = x + 5\)
\(x = 5\)
Now \(\overline {JE} \) is defined by \(x + 5\), and with \(x = 5\), we conclude that \(JE = 10\).
Below you can download some free math worksheets and practice.
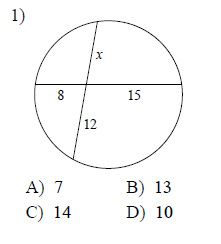
Solve for x. Assume that lines which appear tangent are tangent.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch bellow how to solve this example:
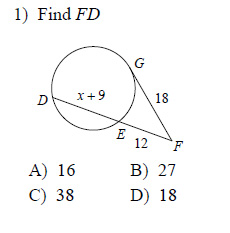
Find the measure of the line segment indicated. Assume that lines which appear tangent are tangent.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch bellow how to solve this example:
Find the measure of the line segment indicated. Assume that lines which appear tangent are tangent.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch bellow how to solve this example:


