Equations
When faced with a rational equation, we encounter two difficulties. The first difficulty we face is that we are dealing with equations with complication expressions in denominators. Secondly, we face the possibility of what are known as extraneous solutions, that is, false solutions that appear. In this article we will deal with both difficulties.
Let’s try to solve for \(a\) in the following equation:
\(\Large \frac{{a - 3}}{{2{a^2} + 18a + 28}} + \Large \frac{1}{{2{a^2} + 18a + 28}} = \Large \frac{1}{{{a^2} + 9a + 14}}\)
We should try to multiply both sides of the equation by some expressions or numbers which would eliminate our denominators. But what? If we do some factoring, the answer will become clearer:
\(\Large \frac{{a - 3}}{{2{a^2} + 18a + 28}} + \Large \frac{1}{{2{a^2} + 18a + 28}} = \Large \frac{1}{{{a^2} + 9a + 14}}\)
\(\Large \frac{{a - 3}}{{2\left( {{a^2} + 9a + 14} \right)}} + \Large \frac{1}{{2\left( {{a^2} + 9a + 14} \right)}} = \Large \frac{1}{{{a^2} + 9a + 14}}\)
Hopefully you can see that all three terms in this equation contain the expression \({a^2} + 9a + 14\). If we multiply both sides of the equation by that expression, we will do some major cancelling in our denominators.
\(\Large \frac{{a - 3}}{{2\left( {{a^2} + 9a + 14} \right)}} + \Large \frac{1}{{2\left( {{a^2} + 9a + 14} \right)}} = \Large \frac{1}{{{a^2} + 9a + 14}}\)
\(\left( {{a^2} + 9a + 14} \right)\left( {\Large \frac{{a - 3}}{{2\left( {{a^2} + 9a + 14} \right)}} + \Large \frac{1}{{2\left( {{a^2} + 9a + 14} \right)}}} \right) = \left( {\Large \frac{1}{{{a^2} + 9a + 14}}} \right)\left( {{a^2} + 9a + 14} \right)\)
\(\Large \frac{{a - 3}}{2} + \Large \frac{1}{2} = 1\)
Wow! That operation really cleaned up the equation. Let’s clean up some more by multiplying both sides by 2, and then solving for \(a\)!. We have
\(\Large \frac{{a - 3}}{2} + \Large \frac{1}{2} = 1\)
\(\left( 2 \right)\left( {\Large \frac{{a - 3}}{2} + \Large \frac{1}{2}} \right) = \left( 1 \right)\left( 2 \right)\)
\(a - 3 + 1 = 2\)
\(a - 2 = 2\)
\(a = 4\)
Here we must be careful. When we multiply both sides of an equation by an expression containing variables, we must check for extraneous, or false, solutions. The reasoning behind this has to do with the fact that division by 0 is undefined. You can do more research to learn about extraneous solutions if you wish. But all it boils down to is that we must check the solution we got in our original equation. We have
\(\Large \frac{{4 - 3}}{{2{{\left( 4 \right)}^2} + 18\left( 4 \right) + 28}} + \Large \frac{1}{{2{{\left( 4 \right)}^2} + 18\left( 4 \right) + 28}} = \Large \frac{1}{{{4^2} + 9\left( 4 \right) + 14}}\)
\(\Large \frac{1}{{32 + 72 + 28}} + \Large \frac{1}{{32 + 72 + 28}} = \Large \frac{1}{{16 + 36 + 14}}\)
\(\Large \frac{1}{{132}} + \Large \frac{1}{{132}} = \Large \frac{1}{{66}}\)
\(\Large \frac{2}{{132}} = \Large \frac{1}{{66}}\)
\(\Large \frac{1}{{66}} = \Large \frac{1}{{66}}\)
The solution checks. Therefore \(a = 4\) is a solution to our original equation. Let’s look at another example. We want to solve for \(p\) in
\(\Large \frac{8}{{p - 5}} = 1 + \Large \frac{1}{{p - 5}}\)
First multiply both sides by \(p - 5\)
\(\left( {p - 5} \right)\left( {\Large \frac{8}{{p - 5}}} \right) = \left( {p - 5} \right)\left( {1 + \Large \frac{1}{{p - 5}}} \right)\)
\(8 = p - 5 + 1\)
\(8 = p - 4\)
\(p = 12\)
Again, check for extraneous solutions
\(\Large \frac{8}{{12 - 5}} = 1 + \Large \frac{1}{{12 - 5}}\)
\(\Large \frac{8}{7} = 1 + \Large \frac{1}{7}\)
\(\Large \frac{8}{7} = \Large \frac{8}{7}\)
The solution checks. So \(p = 12\) is a solution to the original equation.
Below you can download some free math worksheets and practice.
Solve each equation. Remember to check for extraneous solutions.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
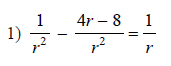
Watch below how to solve this example:
Solve each equation. Remember to check for extraneous solutions.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
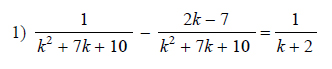
Watch below how to solve this example:
Solve each equation. Remember to check for extraneous solutions.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
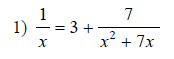
Watch below how to solve this example:


