Absolute value equations
When faced with an absolute value equation, we need to correctly utilize the definition of absolute value.
Definition: Let \(x\) be some variable or algebraic expression. Then
\(\left| x \right| = \left\{ {\begin{array}{*{20}{c}}
{ - x, if x < 0} \\
{x, if x \geqslant 0}
\end{array}} \right.\)
We can state this in the form of an equation as
\(\left| x \right| = a \Leftrightarrow x = - a{\text{ or }}x = a\)
That is, if \(x\) is a negative number, then the absolute value of \(x\) its opposite. But if \(x\) is a positive number, then the absolute value of \(x\) is itself. Unless \(x = 0\), every absolute value equation should have two solutions. Let’s see if we can solve absolute value equations now.
Example: Solve the equation \(\left| {10x - 1} \right| = 51\)
Solution: We know that the expression \(\left| {10x - 1} \right|\) has a different result depending on whether \(10x - 1 0\) or \(10x - 1 \geqslant 0\). And we don’t know which one is true in this situation. So we set up two equaions. We have
| \(10x - 1 = - 51\) | or | \(10x - 1 = 51\) |
| \(10x = - 50\) | or | \(10x = 52\) |
| \(x = - 5\) | or | \(x = \Large \frac{{52}}{{10}} = \Large \frac{{26}}{5}\) |
So our solution set for the equation \(\left| {10x - 1} \right| = 51\) is \(\left\{ { - 5,\Large \frac{{26}}{5}} \right\}\).
This may seem a bit confusing at first, but let’s check the answers and you’ll see that they’re true! We have
\(\begin{gathered}
\left| {10\left( { - 5} \right) - 1} \right| = 51 \\
\left| { - 50 - 1} \right| = 51 \\
\left| { - 51} \right| = 51 \\
\end{gathered} \)
This solution is certainly true. Let’s check the other. We have
\(\begin{gathered}
\left| {10\left( {\frac{{26}}{5}} \right) - 1} \right| = 51 \\
\left| {2\left( {26} \right) - 1} \right| = 51 \\
\left| {52 - 1} \right| = 51 \\
\left| {51} \right| = 51 \\
\end{gathered} \)
Another true solution! Hopefully you can see and trust the fact that each absolute value equation has two solutions! Let’s do one more example:
Example: Solve the equation \(\left| { - 6 - p} \right| = 4\).
Solution: This statement implies
| \( - 6 - p = - 4\) | or | \( - 6 - p = 4\) |
| \( - p = 2\) | or | \( - p = 10\) |
| \(p = - 2\) | or | \(p = - 10\) |
So the solution set for the equation \(\left| { - 6 - p} \right| = 4\) is \(\left\{ { - 10, - 2} \right\}\).
Below you can download some free math worksheets and practice.
Solve each equation.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
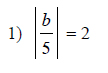
Watch bellow how to solve this example:
Solve each equation.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch bellow how to solve this example:
Solve each equation.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch bellow how to solve this example:


