Circumference and area
Two of the most basic formulas regarding circles are the formulas for area and circumference. The area of a circle is the number of square units that it takes to fill the inside of the circle. The circumference of the circle is the distance around the circle. We state two definitions:
DEFINITION: For a circle with radius r, the area A of the circle is given by
\(A = \pi {r^2}\)
DEFINITION: For a circle with radius r, the circumference C of the circle is given by
\(C = 2\pi r\)
We can use these two formulas to find areas and circumferences of circles. Let’s try it out.
Example: Find the area of the circle whose diameter is 20 inches.
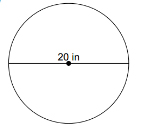
Solution: Before we can find the area of this circle, we need to know its radius. But since the radius is equal to half the diameter, we can conclude that
\(r = \frac{1}{2}\left( {20} \right) = 10\) inches
Then, using the formula for area, we have
\(A = \pi {r^2} = \pi \left( {{{10}^2}} \right)\)
Using the calculator’s value for \(\pi \), we can approximate this as
\(A = \left( {3.141592654} \right)\left( {{{10}^2}} \right)\)
\( = \left( {3.141592654} \right)\left( {100} \right)\)
\( = 314.2{\text{i}}{{\text{n}}^2}\)
Example: Find the area of the circle with diameter 16m.
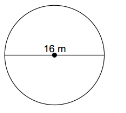
Solution: Again, we need to obtain the radius of this circle. Since the radius is equal to half the diameter, we know that \(r = 8\). Then, using the formula for area, we have
\(A = \pi {r^2}\)
\( = 3.141592654 \times {8^2}\)
\( = 3.141592654 \times 64\)
\( = 201.1{\text{}}{{\text{m}}^2}\)
Below you can download some free math worksheets and practice.
Find the circumference of each circle. Use your calculator's value of π. Round your answer to the nearest tenth.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
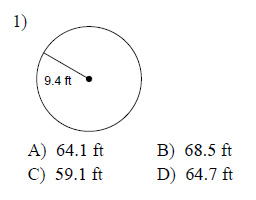
Watch bellow how to solve this example:
Find the area of each. Use your calculator's value of π. Round your answer to the nearest tenth.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
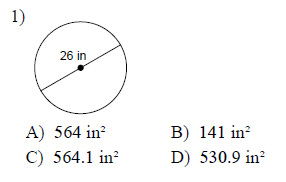
Watch bellow how to solve this example:
Find the circumference of each circle.
This free worksheet contains 10 assignments each with 13 questions with answers.
Example of one question:
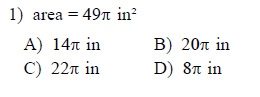
Watch bellow how to solve this example:


