Simplifying and excluded values
One of the first things we would like to do with rational expressions is learn to simplify them. Rational expressions can look rather intimidating, but with a little bit of simplification, we can make them look a whole lot less intimidating.
We do have to watch out for excluded values when we are dealing with rational expressions. Excluded values are those values of the variable which would cause the denominator to be 0. This is not allowed, since division by 0 is undefined. So as we work to simplify these rational expressions, we must be careful to state the excluded values.
Let’s take a look at an example. Simplify the expression
\(\Large \frac{{{r^2} - 15r + 50}}{{{r^2} - 3r - 70}}\)
The first thing we should do is factor the polynomials in both the numerator and the denominator. If we are lucky, we will find one or more common factors that can cancel. We have
\(\Large \frac{{{r^2} - 15r + 50}}{{{r^2} - 3r - 70}} = \Large \frac{{\left( {r - 10} \right)\left( {r - 5} \right)}}{{\left( {r - 10} \right)\left( {r + 7} \right)}}\)
The polynomials do factor! Okay, before we go any further we want to state the excluded values of this rational expression. Again, excluded values are those values that would cause the denominator to be 0. In our case, the excluded values would be those values of \(r\) such that \({r^2} - 3r - 70\) or \(\left( {r - 10} \right)\left( {r + 7} \right)\) is 0. We set \(\left( {r - 10} \right)\left( {r + 7} \right) = 0\) and we have the excluded values are -7 and 10. Now let’s finish simplifying this rational expression by cancelling the common factor \(\left( {r - 10} \right)\). We have
\(\Large \frac{{{r^2} - 15r + 50}}{{{r^2} - 3r - 70}} = \Large \frac{{\left( {r - 10} \right)\left( {r - 5} \right)}}{{\left( {r - 10} \right)\left( {r + 7} \right)}}\), with \(r \ne - 7,10\)
\( = \Large \frac{{r - 5}}{{r + 7}}\), with \(r \ne - 7,10\)
We have just simplified a rational expression! Let’s try another example. We want to simplify the expression
\(\Large \frac{{{m^2} - 4m - 5}}{{5m + 5}}\)
Let’s begin again by doing any factoring that we can do. We have
\(\Large \frac{{{m^2} - 4m - 5}}{{5m + 5}} = \Large \frac{{\left( {m - 5} \right)\left( {m + 1} \right)}}{{5\left( {m + 1} \right)}}\)
Now we see that there is a common factor of \(\left( {m + 1} \right)\) that we can cancel. We also should be able to see that the excluded value is -1 (since \(m = - 1\) would result in the denominator being 0). We finish the problem:
\(\Large \frac{{{m^2} - 4m - 5}}{{5m + 5}} = \Large \frac{{\left( {m - 5} \right)\left( {m + 1} \right)}}{{5\left( {m + 1} \right)}}\), with \(m \ne - 1\)
\( = \Large \frac{{m - 5}}{5}\), with \(m \ne - 1\)
Below you can download some free math worksheets and practice.
Simplify each and state the excluded values.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
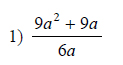
Watch below how to solve this example:
Simplify each and state the excluded values.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
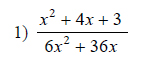
Watch below how to solve this example:
Simplify each and state the excluded values.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
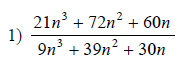
Watch below how to solve this example:


