Angle bisectors
An angle bisector is a line that cuts an angle in half.
Example 1:
If \(\overrightarrow {BD} \) is an angle bisector, find \(\angle ADB\) & \(\angle ADC\).
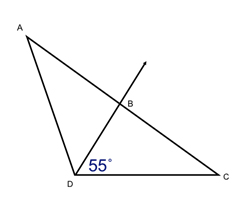 Since the angle bisector cuts the angle in half, the other half must also measure 55°.
Since the angle bisector cuts the angle in half, the other half must also measure 55°.
\(\angle ADB = {\text{55}}^\circ \)
Add both of these angles together to get the whole angle.
\(\angle ADB + \angle BDC = \angle ADC\)
\({\text{55}}^\circ + {\text{55}}^\circ = {\text{ 11}}0^\circ \)
\(\angle ADC = {\text{11}}0^\circ \)
Let’s try a tougher one.
Example 2:
\(\overline {DP} \) is an angle bisector. Find x if \(m\angle 1 = 6x + 5\) & \(m\angle 2 = 5x + 12\)
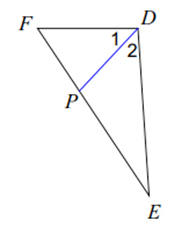
\(m\angle 1 = m\angle 2\)
\({\text{6}}x + {\text{ 5 }} = {\text{ 5}}x + {\text{ 12}}\)
\(x + {\text{ 5 }} = {\text{ 12}}\)
\(x = {\text{ 7}}\)
Now, there are three angles in a triangle, so all together a triangle can have three different angle bisectors. These lines will all meet together inside the triangle. Lines are called concurrent if they all meet and the point of concurrency of the three angle bisectors is called an incenter. It’s called an incenter because if you were to draw a circle that fits inside the triangle, the angle bisectors would always meet directly “in the center” of the circle. Here’s a few diagrams showing the angle bisectors and their incenter.
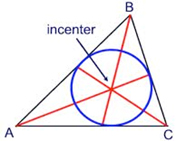
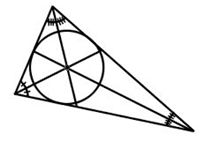
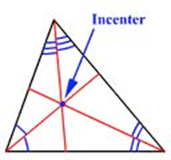
We have these lines for a reason. They serve a purpose in math as well as real life. The special property that the incenter has is that it’s perpendicular distance to all three sides of the triangle are the same. We use the word equidistant for this. So, the incenter is equidistant from all three sides of the triangle when it is crossed at a 90°angle. Maybe a picture with help:
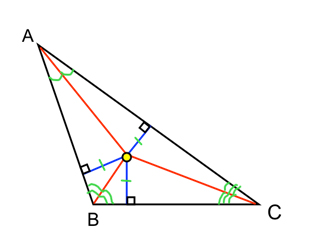
Ok, so the red lines are the angle bisectors, the yellow circle is the incenter, and the blue lines are the equidistant lines. Those blue lines will always have equal measures.
Example 3:
D is the incenter of the triangle. \(\overline {DE} = 2x + 4\) & \(\overline {DF} = 4x - 6\). Find x and the measure of \(\overline {DG} \).
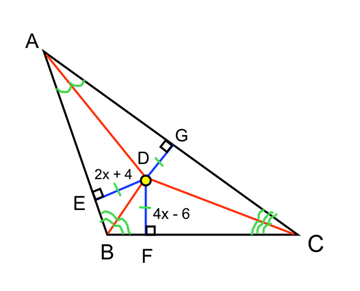
\(\overline {DE} = \overline {DF} \)
\(2x + 4 = 4x - 6\)
\({\text{4 }} = {\text{ 2}}x--{\text{ 6}}\)
\({\text{1}}0 = {\text{2}}x\)
\({\text{5 }} = x\)
\(\overline {DG} \) is going to be the same measure as \(\overline {DE} \) & \(\overline {DF} \). Take x and plug it into one of the equations to find the measure of \(\overline {DG} \).
\({\text{2}}x + {\text{ 4 }} = \overline {DG} \)
\({\text{2}}\left( {\text{5}} \right){\text{ }} + {\text{ 4 }} = \overline {DG} \)
\({\text{1}}0{\text{ }} + {\text{ 4 }} = \overline {DG} \)
\({\text{14}} = \overline {DG} \)
Below you can download some free math worksheets and practice.
Each figure shows a triangle with one of its angle bisectors.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
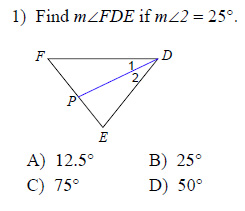
Watch below how to solve this example:
Each figure shows a triangle with one of its angle bisectors.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:

Watch below how to solve this example:
Each figure shows a triangle with its three angle bisectors intersecting at point P.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
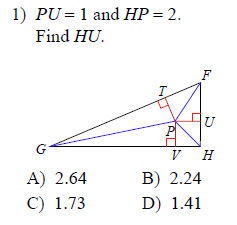
Watch below how to solve this example:


