Operations and scientific notation
Before we begin, let’s restate the properties of exponents so that we have them available to use in the examples.
Properties of Exponents
- Zero Exponent Property \(\Large {a^0} = 1, a \ne 0\)
- Negative Exponent Property \(\Large {a^{ - b}} = \frac{1}{{{a^b}}}, a \ne 0\)
- Product of Powers Property \(\Large {a^b} \cdot {a^c} = {a^{b + c}}, a \ne 0\)
- Quotient of Powers Property \(\Large \frac{{{a^b}}}{{{a^c}}} = {a^{b - c}}\) \(a \ne 0\)
- Power of a Product Property \(\Large {a^c} \cdot {b^c} = {\left( {ab} \right)^c}, a,b \ne 0\)
- Power of a Quotient Property \(\Large \frac{{{a^c}}}{{{b^c}}} = {\left( {\frac{a}{b}} \right)^c}, a,b \ne 0\)
- Power of a Power Property \(\Large {\left( {{a^b}} \right)^c} = {a^{bc}}\)
- Rational Exponent Property \(\Large {a^{\frac{1}{b}}} = \sqrt[b]{a}, b \ne 0\)
- \(\Large {a^{\frac{c}{b}}} = \sqrt[b]{{{a^c}}} = {\left( {\sqrt[b]{a}} \right)^c}\)
Now we want to use these properties to solve problems involving scientific notation. There is nothing to be worried about here. Just remember that in scientific notation, the \( \times \) stands for multiplication, just like it did back in third and fourth grade. Don’t let the look of the problem intimidate you. Let’s jump straight to an example.
Example: Simplify
\(\large \frac{{4 \times {{10}^{ - 2}}}}{{3.01 \times {{10}^{ - 2}}}}\)
Write your answer in scientific notation.
Solution: We use the properties of exponents.
| \(\large \frac{{4 \times {{10}^{ - 2}}}}{{3.01 \times {{10}^{ - 2}}}} = \frac{4}{{3.01}} \cdot \frac{{{{10}^{ - 2}}}}{{{{10}^{ - 2}}}}\) | |
| \(\large = \frac{4}{{3.01}} \cdot {10^{ - 2 - \left( { - 2} \right)}}\) | Quotient of Powers Property |
| \(\large = \frac{4}{{3.01}} \cdot {10^0}\) | |
| \(\large = \frac{4}{{3.01}} \cdot 1,\) | Zero Exponent Property |
| \( = 1.329\) | Rounded to three decimal places |
| \( = 1.329 \times {10^0}\) | Scientific notation required,and \({10^0} = 1\) |
Now we did a few extra steps in the problem above, but it is important to take our time in the beginning, and make sure we are doing the problems the right way.
Example: Simplify
\(\left( {8.8 \times {{10}^4}} \right)\left( {8 \times {{10}^{ - 6}}} \right)\)
Write your answer in scientific notation.
Solution: We use the properties of exponents.
| \(\left( {8.8 \times {{10}^4}} \right)\left( {8 \times {{10}^{ - 6}}} \right) = \left( {8.8} \right)\left( 8 \right)\left( {{{10}^4}} \right)\left( {{{10}^{ - 6}}} \right)\) | |
| \( = \left( {8.8} \right)\left( 8 \right)\left( {{{10}^{4 + \left( { - 6} \right)}}} \right),\) | Product of Powers Property |
| \( = \left( {8.8} \right)\left( 8 \right)\left( {{{10}^{ - 2}}} \right)\) | |
| \( = \left( {8.8} \right)\left( 8 \right)\left( {{{10}^{ - 2}}} \right)\) | |
| \( = 7.04\left( {10} \right)\left( {{{10}^{ - 2}}} \right),\) | Working toward scientific notation |
| \( = 7.04\left( {{{10}^{1 + \left( { - 2} \right)}}} \right),\) | Product of Powers Property |
| \( = 7.04 \times {10^{ - 1}},\) | Scientific Notation |
Below you can download some free math worksheets and practice.
Simplify. Write each answer in scientific notation.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
![]()
Watch bellow how to solve this example:
Simplify. Write each answer in scientific notation.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
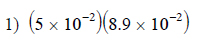
Watch bellow how to solve this example:
Simplify. Write each answer in scientific notation.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
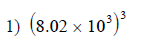
Watch bellow how to solve this example:


