Multiplying
To multiply radical expressions, we follow the typical rules of multiplication, including such rules as the distributive property, etc. There is one property of radicals in multiplication that is important to remember. So let’s look at it.
Definition: \(\left( {a\sqrt b } \right) \cdot \left( {c\sqrt d } \right) = ac\sqrt {bd} \)
Example of the Definition: Consider the expression \(\left( {2\sqrt 3 } \right)\left( {4\sqrt 5 } \right)\). According to the definition above, the expression is equal to \(8\sqrt {15} \).
Essentially, this definition states that when two radical expressions are multiplied together, the corresponding parts multiply together. That is, numbers outside the radical multiply together, and numbers inside the radical multiply together.
Let’s try an example. Simplify the expression
\(\sqrt 3 \left( {2 - 3\sqrt 6 } \right)\)
Here we must remember to use the distributive property of multiplication, just like anytime. But then we will use our property of multiplying radicals to handle the radical parts. We have
\(\sqrt 3 \left( {2 - 3\sqrt 6 } \right) = 2\sqrt 3 - 3\sqrt {18} \)
Now since \(18 = 2 \cdot {3^2}\), we can simplify the expression one more step. We have
\(\sqrt 3 \left( {2 - 3\sqrt 6 } \right) = 2\sqrt 3 - 3\sqrt {18} \)
\( = 2\sqrt 3 - 3 \cdot 3\sqrt 2 \)
\( = 2\sqrt 3 - 9\sqrt 2 \)
So we see that multiplying radicals is not too bad. Let’s try one more example. We want to simplify the expression
\(\sqrt 3 \left( {4\sqrt {10} + 4} \right)\)
Again, we want to use the typical rules of multiplying expressions, but we will additionally use our property of radicals, remembering to multiply component parts. We have
\(\sqrt 3 \left( {4\sqrt {10} + 4} \right) = 4\sqrt {30} + 4\sqrt 3 \)
Below you can download some free math worksheets and practice.
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
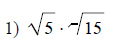
Watch below how to solve this example:
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
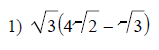
Watch below how to solve this example:
Simplify.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
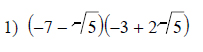
Watch below how to solve this example:


