Proving triangles congruent
Two triangles are congruent if all six parts have the same measures. The three angles and the three sides must match. There is, however, a shorter way to prove that two triangles are congruent! In some cases, we are allowed to say that two triangles are congruent if a certain 3 parts match because the other 3 MUST be the same because of it. There are five of these certain cases and they are called postulates, which basically just means a rule.
1. Side-Side-Side (SSS)
If we know that the three sides of a triangle are congruent to the three sides of another triangle, then the angles MUST be the same (or it wouldn’t form a triangle).
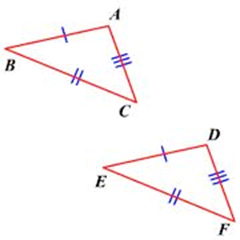
\(\overline {AB} \cong \overline {DE} \) (side)
\(\overline {AC} \cong \overline {DF} \) (side)
\(\overline {BC} \cong \overline {EF} \) (side)
\(\therefore \Delta ABC \cong \Delta DEF\)
The symbol \(\therefore \) means “therefore.” If we are able to show that the three corresponding sides are congruent, then we have enough information to prove that the two triangles are congruent because of the SSS Postulate!
2. Side-Angle-Side (SAS)
If we can show that two sides and the angle IN BETWEEN them are congruent, then the whole triangle must be congruent as well. It looks like this:
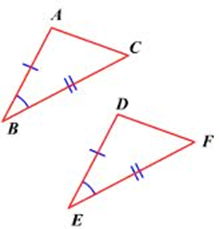
\(\overline {AB} \cong \overline {DE} \) (side)
\(\angle B \cong \angle E\) (angle)
\(\overline {BC} \cong \overline {EF} \) (side)
\(\therefore \Delta ABC \cong \Delta DEF\)
The angle HAS to be in between the two sides for the SAS Postulate to be used.
3. Angle-Side-Angle (ASA)
If we can show that two angles and the side IN BETWEEN them are congruent, then the whole triangle must be congruent as well.
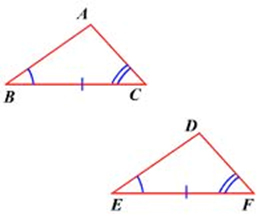
\(\angle B \cong \angle E\) (angle)
\(\overline {BC} \cong \overline {EF} \) (side)
\(\angle C \cong \angle F\) (angle)
\(\therefore \Delta ABC \cong \Delta DEF\)
The side HAS to be in between the two angles for the ASA Postulate to be used.
4. Angle-Angle-Side (AAS)
If the side is not in between the angles, it’s actually still okay, but you must use the AAS Postulate.
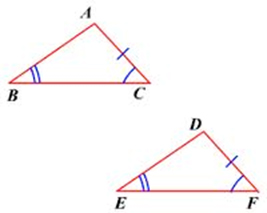
\(\angle B \cong \angle E\) (angle)
\(\angle C \cong \angle F\) (angle)
\(\overline {AC} \cong \overline {DF} \) (side)
\(\therefore \Delta ABC \cong \Delta DEF\)
5. Hypotenuse-Leg (HL)
This one is a little bit different. It can only be used in a right triangle. So, if the two triangles are both right triangles and one of their corresponding legs are congruent as well as their hypotenuse, then they are congruent by the HL Postulate.
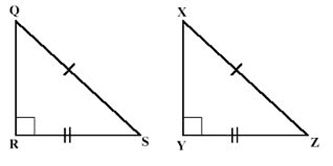 \(\Delta QRS\& \Delta XYZ\) are right triangles
\(\Delta QRS\& \Delta XYZ\) are right triangles
\(\overline {QS} \cong \overline {XZ} \) (hypotenuse)
\(\overline {RS} \cong \overline {YZ} \) (leg)
\(\therefore \Delta QRS \cong \Delta XYZ\)
If you don’t have one of these above postulates, then you don’t have enough information to assume that the triangles are congruent.
You CANNOT use Angle-Angle-Angle because two triangles can have the same angles but have completely different sides, like the following example:
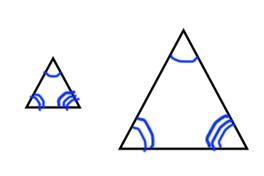
Not Congruent!
You also CANNOT use Side-Side-Angle because it doesn’t guarantee that the triangles will be completely congruent.
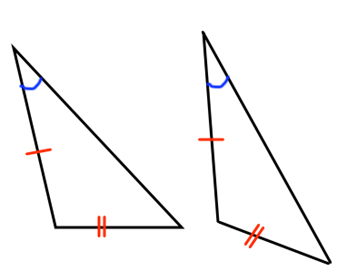
Not Congruent!
Below you can download some free math worksheets and practice.
State if the two triangles are congruent. If they are, state how you know.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
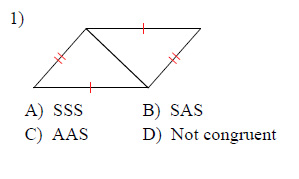
Watch below how to solve this example:
State if the two triangles are congruent. If they are, state how you know.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
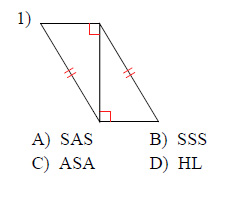
Watch below how to solve this example:
State what additional information is required in order to know that the triangles are congruent for the reason given.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
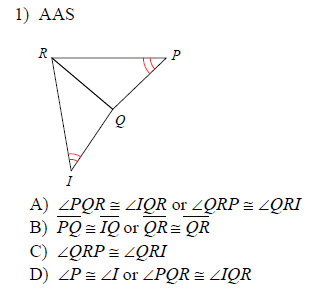
Watch below how to solve this example:


