Solving by elimination
We have learned how to solve an equation when there is only one variable to consider. What happens if there are two? We can still solve for both variables but will need two equations. This is called a system of equations. Here’s an example:
\(2x - 9y = - 12\)
\(3x + 18y = - 18\)
We will be able to solve for both “x” and “y” but only one at a time. We need to cancel out or eliminate a variable first. We are allowed to add these two equations by combining like terms but we want one of our variables to cancel out at the same time. Sounds like a lot to worry about, right? Let’s take it one step at a time.
We want something to cancel out which means the coefficients will have to be the same number but one has to be positive and one has to be negative. In our example, we are close with a -9y in the top one and a +18y in the bottom. What would we have to multiply the top equation by to make it a -18y? It would be 2! We have to multiply both sides of the equation by 2.
\(2(2x - 9y) = 2( - 12)\) \( \to \) \(4x - 18y = - 24\)
Now our system of equations looks like this, and we can add them.
\(4x - 18y = - 24\)
+ \(3x + 18y = - 18\)
__________________
\(7x = - 42\)
Divide both sides by 7 and:
\(x = - 6\)
Great! We’ve solved for one of the variables. To solve for the other, take an original equation and plug in -6 for x.
\(2x - 9y = - 12\)
\(2( - 6) - 9y = - 12\)
\( - 12 - 9y = - 12\)
+12 +12
\( - 9y = 0\)
\(y = 0\)
We have solved our system of equations! We found x to equal -6 and y to equal 0. We can put our answers in coordinate form of (x,y) and we have the point (-6,0) which is where both of these lines (equations) intersect or cross.
Let’s try one more.
\(20x + 7y = - 29\)
\( - 10x - 5y = 25\)
This time the coefficients of x are closer to the same number but with opposite signs. We can multiply the bottom equation by 2 to get them to cancel out.
\(2( - 10x - 5y) = 2(25)\) \( \to \) \( - 20x - 10y = 50\)
Now we have:
\(20x + 7y = - 29\)
+ \( - 20x - 10y = 50\)
_________________
\( - 3y = 21\)
Divide both sides by -3 and we get:
\(y = - 7\)
Now remember, you’re not done! Let’s plug our “y” in to one of our equations.
\(20x + 7y = - 29\)
\(20x + 7( - 7) = - 29\)
\(20x + - 49 = - 29\)
+49 +49__
\(20x = 20\)
\(x = 1\)
Our coordinate point is (1,-7) and we have solved another system of equations!
Below you can download some free math worksheets and practice.
Solve each system by elimination.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
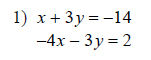
Watch below how to solve this example:
Solve each system by elimination.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
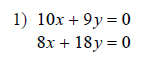
Watch below how to solve this example:
Solve each system by elimination.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
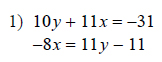
Watch below how to solve this example:


