Graphing exponential functions
When graphing any equation, it is important to keep in mind the general shape of the graph. For instance, the general shape of the graph of \(y = {x^2}\) is a parabola, and the general shape of the graph of \(y = \left| x \right|\) is a \(V\).
Similarly, the graphs of exponential equations have a general shape. It looks like this:
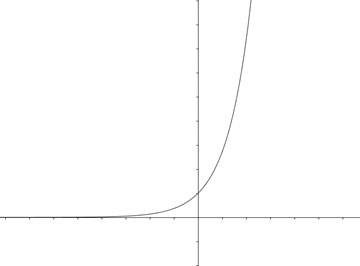
Note that the graph has a curved shape. Also note that as the graph continues farther toward negative infinity, it becomes indistinguishable from the x-axis. In fact, the graph will continue to get closer and closer to the x-axis without ever crossing it. In this situation, the x-axis is known as an asymptote. You can do research to learn more about what an asymptote is.
We must keep in mind the general shape of the graph so that when we plot several points and connect the dots, we connect them properly.
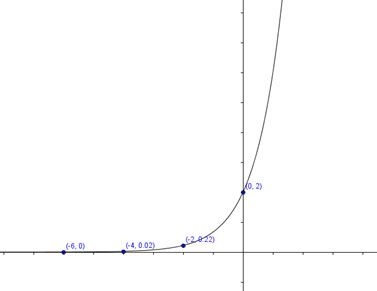
Example: Sketch the graph of \(y = 2 \cdot {3^x}\)
Solution: Here we should plot at least 5 or 6 points to get a good grip on what this graph looks like. We have
| \(x\) | \(y = 2 \cdot {3^x}\) |
| -6 | 0,00274 |
| -4 | 0,02469 |
| -2 | 0,22222 |
| 0 | 2 |
| 2 | 18 |
| 4 | 162 |
The graph is below. Several of the points are so far from the others that it is not convenient to plot them. This is true of almost all exponential equations. They grow so fast in both directions that it is hard to plot more than a few points.
Let’s try one more example.
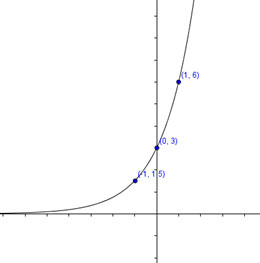
Example: Sketch the graph of \(y = 3 \cdot {2^x}\)
Solution: Let’s plot some values, remembering the general shape of an exponential graph.
| \(x\) | \(y = 3 \cdot {2^x}\) |
| -1 | 1,5 |
| 0 | 3 |
| 1 | 6 |
Here is the graph. You may always plot as many points as you need to see the graph.
Below you can download some free math worksheets and practice.
Sketch the graph of each function.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:

Watch bellow how to solve this example:
Sketch the graph of each function.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:

Watch bellow how to solve this example:
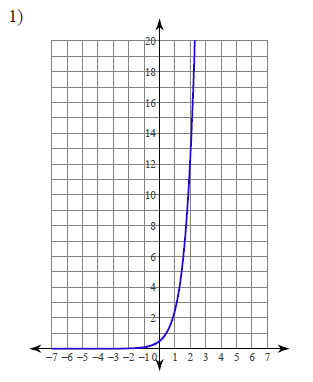
Write an equation for each graph.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
Watch bellow how to solve this example:


