Solving by graphing
Systems of equations, if they have a solution, will yield values for \(x\) and \(y\) that satisfy both of the equations at the same time. Graphically, this value corresponds to the point of intersection of the two lines represented by the equations. To solve a system of equations by graphing:
- Graph both lines in the coordinate plane
- The point of intersection is the solution to the system
- If the lines are parallel, there is no solution
- If the lines intersect at a single point, there is one solution
- If the lines coincide (in effect, they are the same line), then there are infinitely many solutions.
Let’s try an example.
Example: Solve the system by graphing
\(y = - \Large \frac{2}{3}x + 5\)
\(y = \Large \frac{2}{9}x - 3\)
Solution: Conveniently, both of the equations are given in slope intercept form. So we graph both of the equations in the coordinate plane.
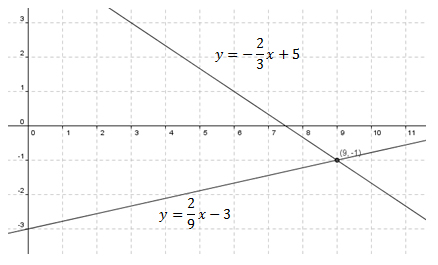
We see that the point of intersection between the two lines is (9, -1). Then (9, -1) s the solution to the system.
Example: Solve the system by graphing
\(y = - \Large \frac{1}{4}x + 4\)
\(y = \Large \frac{5}{2}x - 7\)
Solution:Again, we graph both of the equations in the coordinate plane:
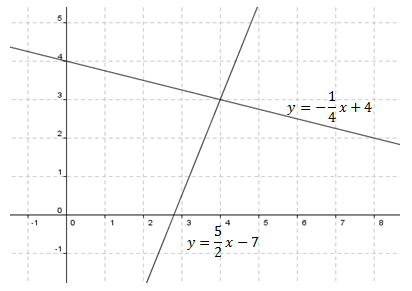
Here we can see that the point of intersection of the two lines is (4, 3). Then (4, 3) is the solution to the system of equations.
You can always check your solution by substituting the values for \(x\) and \(y\) that you obtained into both of the original equations and see if you get a true statement. Sometimes you cannot solve by graphing because it is not precise. Then you will need additional methods to solve these systems.
Below you can download some free math worksheets and practice.
Solve each system by graphing.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
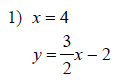
Watch below how to solve this example:
Solve each system by graphing.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
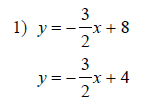
Watch below how to solve this example:
Solve each system by graphing.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
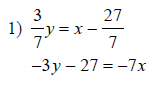
Watch below how to solve this example:


