Absolute value inequalities
Absolute value is the distance a number is from zero. Since it is a distance, it is always positive. This doesn’t mean that your variable has to be positive, but your final answer will be.
When we use inequalities, we have more than one answer that can solve our problem. So if we put absolute value and inequalities together, it means that we will have values in both directions from zero that will solve our problem.
Let’s try a few examples.
Example 1:
\(\left| x \right| \ge 4\)
This is read as, “the absolute value of a number is greater than or equal to 4.” So the distance from zero has to be 4 or greater. This means all numbers greater than or equal to 4 would be our answer. But don’t forget, we could go in the other direction as well. All numbers less than or equal to -4 work as well! Whenever we have absolute value inequalities, we have to split the equation into a positive side and a negative side so that we account for both directions. You have to flip the inequality for the negative side.
\(x \ge 4\) or \(x \le - 4\)
To graph this, we will use closed circles since the answer includes 4 and -4.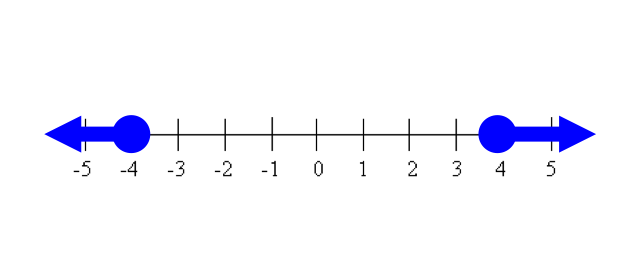
Example 2:
\(\left| {8 + a} \right| \le 2\)
Let’s split it. Don’t forget to flip the sign for the negative inequality.
\(8 + a \le 2\)
-8 -8
\(a \le - 6\)
\(8 + a \ge - 2\)
-8 -8
\(a \ge - 10\)
This time we can squish the two inequalities into one compound inequality and our final answer will look like:
\( - 10 \le a \le - 6\)![]()
“Less than” inequalities will always connect and “greater than” inequalities will shoot off in different directions.
This one has many steps. First, we cannot split the inequality unless the absolute value is all by itself. So we have to add 2 to both sides to get the absolute value alone.
\(\left| {2x + 4} \right| - 2 < 8\)
+2 +2
\(\left| {2x + 4} \right| < 10\)
Now, let’s split the inequality.
\(2x + 4 < 10\)
-4 -4
\(2x < 6\)
\( \div 2\) \( \div 2\)
________________
\(x < 3\)
-4 -4
\(2x > - 14\)
\( \div 2\) \( \div 2\)
________________
\(x > - 7\)
This is a “less than” inequality so we can write it as a compound inequality and they will connect on the graph.
\( - 7 < x < 3\)
Notice that the circles are open this time! This is because the answer can’t be equal to -7 or 3.
Bellow you can download some free math worksheets and practice.
Solve each inequality and graph its solution.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
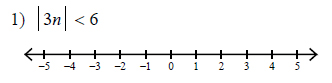
Watch below how to solve this example:
Solve each inequality and graph its solution.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
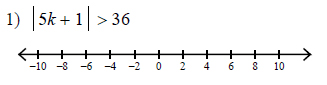
Watch below how to solve this example:
Solve each inequality and graph its solution.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
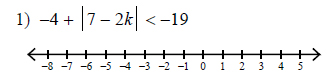
Watch below how to solve this example:


