Writing equations of circles
The general equation of a circle whose center is located at the point \(\left( {h,k} \right)\) and whose radius is \(r\) is given by
\({\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\)
Now we can just plug-n-chug this formula to write the equations of any circle we want.
Example:Write the equation of a circle whose center is \(\left( {6, - 6} \right)\) and with circumference \(2\pi \sqrt {62} \).
Solution: We have the coordinates of the center of the circle. Now we simply need to break down the circumference and figure out what the radius is. We know that
\(Circumference = 2\pi r\)
so that
\(2\pi r = 2\pi \sqrt {62} \)
\(r = \sqrt {62} \)
So the radius is \(\sqrt {62} \). We plug-n-chug:
\({\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\)
\({\left( {x - 6} \right)^2} + {\left( {y - \left( { - 6} \right)} \right)^2} = {\left( {\sqrt {62} } \right)^2}\)
\({\left( {x - 6} \right)^2} + {\left( {y + 6} \right)^2} = 62\)
Then the general equation of the circle with the information given is
\({\left( {x - 6} \right)^2} + {\left( {y + 6} \right)^2} = 62\)
EXAMPLE: Write the equation of the circle with center \(\left( {4,6} \right)\) and circumference \(8\pi \).
SOLUTION: We have
\(circumference = 2\pi r\)
so that
\(2\pi r = 8\pi \)
\(r = 4\)
Then the equation is
\({\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\)
\({\left( {x - 4} \right)^2} + {\left( {y - 6} \right)^2} = 16\)
Below you can download some free math worksheets and practice.
Use the information provided to write the equation of each circle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
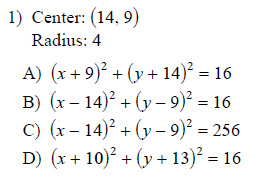
Watch bellow how to solve this example:
Use the information provided to write the equation of each circle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
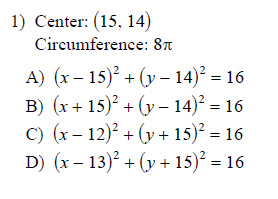
Watch bellow how to solve this example:
Use the information provided to write the equation of each circle.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
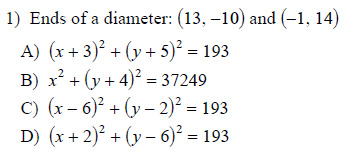
Watch bellow how to solve this example:


