Solving by substitution
Sometimes it is not possible or convenient to solve a system of equations by graphing. In such a case we can turn to a method known as substitution to find the values of the variables. To use the substitution method, we use the following procedure:
- Choose either of the two equations to begin with
- Solve for one of the variables in terms of the other
- Substitute the expression into the other equation
- You will obtain the value of one of the variables
- Substitute this value into either of the original equations to obtain the value of the other variable.
Let’s jump to an example.
Example: Solve the system by substitution
\( - 8x + 5y = - 6\)
\( - 3x + y = - 4\)
Solution: We follow the first procedure. We want to choose either of the two equations to begin with. We choose the second equation because it is easier to solve for the variable \(y\) in that equation. Solving for \(y\) in the second equation gives us
\( - 3x + y = - 4\)
\(y = 3x - 4\)
Continuing the procedure, we substitute the expression \(3x - 4\) for \(y\) in the other original equation. We have
\( - 8x + 5y = - 6\)
\( - 8x + 5\left( {3x - 4} \right) = - 6\)
\( - 8x + 15x - 20 = - 6\)
\(7x - 20 = - 6\)
\(7x = 14\)
\(x = 2\)
We have obtained a value for one of the variables. We substitute this value into either of the original equations. We will substitute it into the second original equation:
\( - 3x + y = - 4\)
\( - 3\left( 2 \right) + y = - 4\)
\( - 6 + y = - 4\)
\(y = 2\)
The solution is (2, 2)
Another Example: Solve the system by substitution
\(7x + y = - 15\)
\( - 6x - 7y = - 24\)
Solution: Here we choose to begin work with the first equation, solving for \(y\). We have
\( - 6x - 7y = - 24\)
\( - 6x - 7\left( { - 7x - 15} \right) = - 24\)
\( - 6x + 49x + 105 = - 24\)
\(43x + 105 = - 24\)
\(43x = - 129\)
\(x = - 3\)
We substitute this value into either of the original equations. We choose the first equation. We have
\(7x + y = - 15\)
\(7\left( { - 3} \right) + y = - 15\)
\( - 21 + y = - 15\)
\(y = 6\)
The solution is (-3, 6).
Below you can download some free math worksheets and practice.
Solve each system by substitution.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
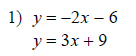
Watch below how to solve this example:
Solve each system by substitution.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
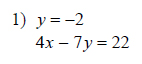
Watch below how to solve this example:
Solve each system by substitution.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
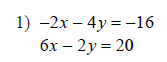
Watch below how to solve this example:


