Arc length and sector area
We can use our knowledge about the area of a circle to help us find the area of a sector. We know that the area of a circle is given by
\(A = \pi {r^2}\)
but if a sector is only a part of a circle, we can just find the area of the part. For example, since a full rotation of a circle is \(2\pi \) radians, we know that any smaller angle would be a fractional part of \(2\pi \). For example,
\(\pi radians \times \Large \frac{{1revolution}}{{2\pi radians}} = \Large \frac{\pi }{{2\pi }}revolutions = \Large \frac{1}{2}revolution\)
That is, the angle \(\pi \) radians is \(\frac{1}{2}\) of a revolution. Let’s generalize this:
\(\theta {\text{}}radians \times \Large \frac{{1{\text{}}revolution}}{{2\pi radians}} = \Large \frac{\theta }{{2\pi }}revolution\)
Then a sector whose angle measure is \(\theta \) is exactly \(\Large \frac{\theta }{{2\pi }}\) of a circle.
Then the area of a sector is \(\frac{\theta }{{2\pi }}\) times the area of a circle. That is,
\({A_{sector}} = \Large \frac{\theta }{{2\pi }} \times {A_{circle}}\)
\( = \Large \frac{\theta }{{2\pi }} \cdot \pi {r^2}\)
\( = \Large \frac{{\theta {r^2}}}{2}\)
Example: Find the area of the sector
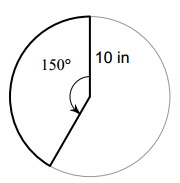
Solution: We just need to substitute the angle and the radius into our formula. But first we note that
\(150^\circ \times \Large \frac{{\pi radians}}{{180^\circ }} = \Large \frac{{5\pi }}{6}radians\)
Then \(A = \Large \frac{\theta }{2}{r^2} = \Large \frac{1}{2}\left( {\Large \frac{{5\pi }}{6}} \right)\left( {{{10}^2}} \right) = \Large \frac{{500\pi }}{{12}} = \Large \frac{{125\pi }}{3}i{n^2}\)
Example: Find the area of the sector.
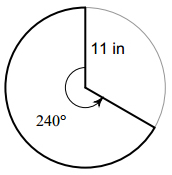
Solution: Again, we need to simply substitute our angle and radius into our formula. But we first need to convert \(240^\circ \) into radians. We have \(240^\circ \times \Large \frac{{\pi radians}}{{180^\circ }} = \Large \frac{{4\pi }}{3}radians\)
Then the area of the sector is
\(A = \Large \frac{\theta }{2}{r^2} = \Large \frac{1}{2} \cdot \Large \frac{{4\pi }}{3} \cdot {11^2} = \Large \frac{{484\pi }}{6} = \Large \frac{{242\pi }}{3}i{n^2}\)
Below you can download some free math worksheets and practice.
Find the length of each arc. Round your answers to the nearest tenth.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
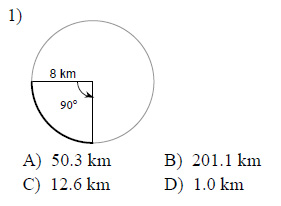
Watch below how to solve this example:
Find the area of each sector.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
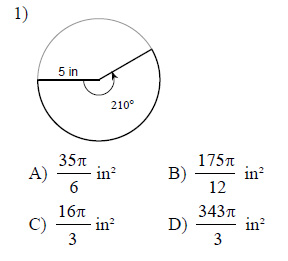
Watch below how to solve this example:
Find the area of each sector.
This free worksheet contains 10 assignments each with 24 questions with answers.
Example of one question:
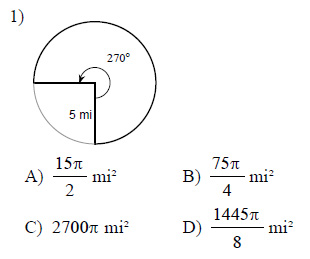
Watch below how to solve this example:


